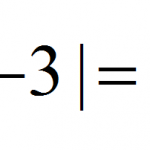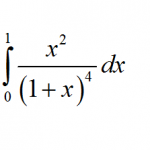Why It Is Not Difficult To Solve Inequalities In Math

A common problem faced by algebra students is how to make the transition from solving equations to solving inequalities. The instructors and teachers usually do not teach the students enough regarding how equations differ from inequalities and, for this reason, the learners can miss some important elements that would give them a strong grounding in these two concepts.

In terms of solving inequalities, this lack of depth results in a deficiency of confidence among the students. In the subsequent paragraphs, we will focus on depicting the precise differences between equations and inequalities and also why it is easier to solve inequalities than you may think.

Differences Between Equations And Inequalities:

Generally speaking, the main intention of an equation is to find a single value where a particular expression is true. For instance, if there is an equation x + 4 = 6, then it is true only when the value of x is 2. Here, “2” happens to be a single value which satisfies the equation. On the other hand, an inequality is going to consider every possible value of x which will satisfy any given comparison and thus it is different from an equation.

For instance, suppose we have x – 4 > 10, and an inequality will look for every value of x such that the condition x – 4 > 10 holds true. In case 4 is added to each side of the inequality, we will get x > 14. Please note that x > 14 actually describes an unending number of points and each one of them will satisfy the condition x – 4 > 10.

Is There Really a Difference?

Once the difference between the two is clear to you, you will comprehend the fact that there is practically no difference between the processes to solve each one of them. We mention the word “practically” since you need to bear in mind one significant difference which will not apply while solving an equation. In fact, it is imperative to alter the inequality sign’s direction if you divide or multiply each side by any negative number while trying to solve an inequality. In other words, “greater than” will become “less than” and vice versa.

If you want to comprehend this, take into consideration the inequality 3 < 4. The inequality is correct since we are certain about the fact that 3 is less than 4. Moreover, it is known to us that if each side is multiplied by the identical number, the inequality will not be wrong anyway.

Consequently, what will be the outcome if each side is multiplied by a negative two? We will get -6 on the left side and -8 on the right. Now, since the statement -6 < -8 is incorrect, the direction of the sign has to be changed so that we get -6 > -8, which is obviously correct. This is due to the fact that as compared to the positive numbers, the negative ones are in reverse order. In fact, when the absolute value of a negative number is bigger, the number is actually lower.

Conclusion:

It will be feasible to steer clear of the majority of the big errors made by the students if these simple ideas are borne in mind while solving inequalities.