كيفية التحليل
يعد تعلم كيفية التحليل أحد أهم المهارات التي يمكنك تعلمها. يحتوي التخصيم على العديد من التطبيقات , بحيث يسعدك أن تأخذ الوقت الكافي لتعلم كل ما يتعلق به.
عادة ما يكون التخصيم أمرًا مفروغًا منه , ويعتمد على خصائص مختلفة , مثل الملكية التبادلية والرابطية والتوزيعية. تسمح لك هذه الخصائص بالتنقل وتجميع المصطلحات بطريقة مريحة.
مرطبات سريعة حول الملكية التبادلية والرابطية والتوزيعية. للأرقام الحقيقية \(x\) , \(y\) و \(z\) , لدينا الخصائص التالية
(ترابطية الإضافة) \((x+y)+z = x+(y+z)\)
تبادلية الإضافة) \( x + y = y + x\)
(خاصية التوزيع) \( x \cdot (y+z) = x \cdot y + x \cdot z\)
حيث \(+\) و \(\cdot\) هما مجموع وحاصل ضرب الأعداد الحقيقية , على التوالي.
لماذا من المفيد معرفة كيفية التحليل؟
هناك العديد من الأسباب , ولكن أحد أهمها هو أن التحليل إلى عوامل يوفر لنا طريقة سهلة لحل المعادلات. في الواقع , التحليل هو الطريقة التي يجب أن نحل بها المعادلات.
على سبيل المثال , ضع في اعتبارك المعادلة التي نحاول حلها من أجل \(x\):
\[\large xy +xz = 0\]كيف نذهب عن ذلك؟ حسنًا , يمكننا استخدام خاصية التوزيع للحصول على:
\[\large x y + x z = x(y+z) = 0\]لذلك , في هذا التعبير الأخير \( x(y+z) = 0\) لدينا مثال على التحليل. في الواقع , أخذنا التعبير الأولي , \(xy+xz\) وقمنا بتحليله في \( x(y+z)\).
إذن , نحتاج الآن إلى حل معادلة أسهل , وهي \( x(y+z) = 0\). لماذا هو أسهل؟ لأننا نعلم الآن أن حاصل الضرب \( x(y+z)\) يساوي صفرًا , فإن أحد العوامل يجب أن يكون مساويًا للصفر.
لذا , إذا علمنا أن \(y+z = \not 0\) , فإننا نعلم أننا بحاجة إلى الحصول على \(x = 0\).
درس
: تتمثل إحدى ميزات التحليل إلى عوامل في القدرة على كتابة معادلة في صورة مضاعفة لعوامل تساوي الصفر. بعد ذلك , يجب أن يكون أحد العوامل على الأقل صفريًا.
على سبيل المثال , عندما نحتاج إلى حل مشكلة \(x\) في المعادلة التالية:
\[\large 5x + 3x = 0\]لا ندرك أننا في الواقع نأخذ في الحسبان عندما نفعل ذلك
\[\large 5x + 3x = (5+3)x = 8x = 0\]لذلك اختزلنا معادلتنا إلى حاصل ضرب عوامل تساوي الصفر: \(8x = 0\). بما أن أحد العوامل \(8\) لا يساوي الصفر , فإن الحل الوحيد الممكن هو \(x = 0\).
بعبارة أخرى
: إذا كنت تعرف كيفية التحليل , فمن المحتمل أن تعرف ذلك
كيفية حل المعادلات
.
كيفية تحليل كثيرات الحدود إلى عوامل
يجب أن يكون دور العوملة واضحًا الآن , من حيث فائدته في حل المعادلات. المشكلة الوحيدة هي أنه لا توجد استراتيجية عامة واحدة يمكن استخدامها لتحليل جميع التعبيرات الجبرية الممكنة.
لذلك , عادة , يسعدنا تحليل التعبيرات البسيطة نسبيًا , ولكن من الناحية المثالية , نود أن نعرف كيفية تحليل أكبر عدد ممكن من التعبيرات.
يتم الوصول إلى التوازن من خلال فئة عامة جدًا من التعبيرات التي يمكننا , في كثير من الأحيان , التعامل معها بشكل منهجي للغاية. هذه الفئة هي فئة كثيرات الحدود. على سبيل المثال , التعبير
\[\large 2x^2 + 5x + 3\]هي كثيرة الحدود من الدرجة 2. أو التعبير أدناه
\[\large x^3 - 3x^2 + 4x+2\]هي كثيرة الحدود من الدرجة 3.
بشكل عام , تعبير عن النموذج
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\]هي كثيرة الحدود من الدرجة \(n\). بطبيعة الحال , كلما كان التعبير أبسط , كان التبسيط أسهل , لذلك يجب أن نحاول معرفة كيفية تحليل المقادير التربيعية أولاً. هذا هو , كثيرات الحدود من الدرجة الثانية.
مثال 1
حلل التعبير التربيعي التالي إلى عوامل
\[\large x^2 + x - 2\]إجابه:
سيوضح لك هذا المثال , عن قصد , أنه قد يكون من الصعب تحليل حتى أبسط تعبير , مثل التعبير أعلاه. ماذا ستفعل لتحليلها؟
ماذا لو قلت لك , تحتاج إلى إضافة صفر؟ إنه نوع سخيف , أليس كذلك؟ لنرى:
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 \]هل توافق على ما ورد أعلاه؟ لقد أضفت للتو \(0\). لم يتغير شيء. ولكن , ماذا لو أخبرتك أن \(0 = 2x - 2x\)؟ وماذا بعد
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 = x^2 + x + (2x - 2x) - 2 \]كل نفس! إنه يعمل , لأنني أضفت صفرًا , لذلك لم يتغير شيء. لكننا الآن نوسعها ونجمعها:
\[\large x^2 + x - 2 = x^2 + x + 0 - 2 \] \[\large = x^2 + x + (2x - 2x) - 2 \] \[ \large = x^2 + x - 2x + 2x - 2 \] \[\large = x^2 + (x - 2x) + 2x - 2 \] \[\large = x^2 - x + 2x - 2 \] \[\large = x(x-1) + 2(x-1)\] \[\large = (x+2)(x-1)\]إذن , أخيرًا , \(x^2 + x - 2 = (x+2)(x-1)\). مخادع؟ ربما , ولكن هذه طريقة واحدة للقيام بذلك. على الرغم من كونها طريقة ذكية للقيام بذلك , فإننا نفضل طريقة أكثر منهجية.
حلل إلى عوامل تربيعية كثيرة الحدود
الحيل الذكية لطيفة , وكل ذلك , لكن عادة ما نفضل اتباع نهج منظم , لا يفشل أبدًا. بالنسبة إلى كثيرات الحدود التربيعية (كثيرات الحدود من الدرجة 2) , هناك طريقة منهجية لمتابعة عملية التحليل:
الخطوة 1
: بالنظر إلى التعبير التربيعي \(ax^2 + bx + c\) , نحل المعادلة أولاً
الخطوة 2
: إذا كانت الحلول (الجذور) للمعادلة أعلاه حقيقية (حتى إذا كان هناك جذر واحد فقط) , فإننا نسمي هذه الجذور \(x_1\) و \(x_2\). بهذه الجذور نحصل على العوامل التالية:
لذا فإن الحلول \(x_1\) و \(x_2\) تحدد العوامل تمامًا.
بطبيعة الحال , في هذه الحالة , كما هو متوقع , يرتبط حل المعادلة التربيعية ارتباطًا وثيقًا بتحليل المعادلة التربيعية إلى عوامل.
مثال 2
حلل المعادلة التربيعية التالية إلى عوامل
\[\large x^2 - 4x + 3\]عن طريق حساب جذورها.
إجابه:
نبدأ بحل المعادلة التربيعية المقابلة:
\[\large x^2 - 4x + 3 = 0\]باستخدام المشهور والمعروف الصيغة التربيعية :
\[\large\displaystyle x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] \[\large\displaystyle = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3)}}{2(1)} \] \[\large\displaystyle = \frac{4 \pm \sqrt{16 - 12}}{2} \] \[\large\displaystyle = \frac{4 \pm \sqrt{4}}{2} \] \[\large\displaystyle = \frac{4 \pm 2}{2} \]مما يعني أن الحلول (الجذور) هي \(x_1 = 1\) و \(x_2 = 1\). بعد ذلك , يمكن تحليل التعبير التربيعي \(x^2 - 4x + 3\) على النحو التالي:
\[\large x^2 - 4x + 3 = a(x - x_1)(x - x_2) = (x-1)(x-3) \]لاحظ أنه في هذه الحالة , فإن المصطلح الذي يضاعف الحد \(x^2\) هو 1 , لذلك في هذه الحالة \(a = 1\).
تحليل كثيرات الحدود بدرجة أكبر من 2
لذلك , لتحليل كثيرات الحدود من الدرجة الثانية , قمت فقط بحساب جذور المعادلة التربيعية المقابلة. كيف يمكنني تحليل كثيرات الحدود من الدرجة الأعلى ؟؟ باستخدام نفس الطريقة بالضبط .
الخطوة 1:
بالنظر إلى التعبير متعدد الحدود \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\) , نحل المعادلة أولاً
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0 = 0\]
الخطوة 2:
إذا كانت الحلول (الجذور) للمعادلة أعلاه حقيقية (حتى لو تكررت) , فإننا نسمي هذه الجذور \(x_1\), \(x_2\), ..., \(x_n\). بهذه الجذور نحصل على العوامل التالية:
\[\large a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0 = a_n(x - x_1)(x - x_2)\cdots (x - x_n)\]
لذلك , يبدو أنه من السهل أيضًا تحليل كثير الحدود من الدرجة 2 إلى عامل كثير الحدود من الدرجة 10. نظريًا , الإجابة هي نعم.
المشكلة الوحيدة هي أنه لا توجد صيغة جبرية بسيطة وقريبة يمكنها حل الجذور لمعادلة متعددة الحدود من الدرجة 5 أو أعلى.
في بعض الأحيان , يمكننا حل معادلات الدرجة الأعلى بالنظر إلى الرسم البياني , أو حتى باستخدام الآلة الحاسبة. على سبيل المثال , تحقق من الرسم البياني أدناه:
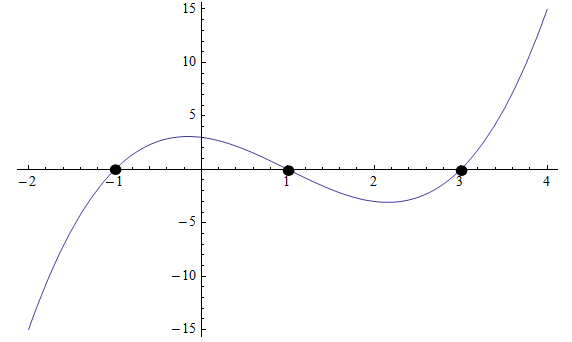
بيانياً , يمكننا أن نرى أن كثير الحدود يعبر المحور x عند ثلاث نقاط: \(x_1 = -1\) و \(x_2 = 1\) و \(x_3 = 3\) , لذلك فهذه هي الجذور.
إذن , نعلم أن كثير الحدود يجب أن يكون على شكل \(p(x) = a(x+1)(x-1)(x-3)\). سنحتاج إلى معرفة نقطة أخرى لمعرفة الثابت \(a\).
المزيد عن العوملة
نحن فقط نخدش السطح بمفهوم العوملة , على الرغم من أنه لا يوجد أكثر مما يمكن فعله للتعبيرات العامة. أفضل ما يمكننا فعله هو إعطاء نهج منظم لعامل كثير الحدود.
ولكن , الحصول على معالجة عامة لكثيرات الحدود ليس بالأمر البسيط , وفكرة استخدام الجذور لتحليل كثير الحدود لا تقل عن النظرية الأساسية للجبر. لذلك , على الأقل من خلال العنوان , يمكنك القول أنه ليس بالقليل.
تحليل العبارات العامة
لا توجد قواعد عامة لتحليل التعبيرات العامة. نحتاج إلى اللعب عن طريق الأذن ومحاولة استغلال بنية التعبير. في بعض الأحيان يمكننا أن نأخذ في الحسبان , وأحيانًا لا نستطيع ذلك. كل هذا يتوقف على التعبير. القاعدة العامة الوحيدة هي محاولة التجميع ومحاولة إيجاد العوامل المشتركة لتجميع وتبسيط أكثر.
كيفية التحليل بالتجميع
هذا هو المثال الأول الذي فعلناه. قل أن لديك:
\[\large x^2 - x + 2x - 2 \]لذلك قمنا بتجميع أول حدين وآخر حدين للحصول على:
\[\large (x^2 - x) + (2x - 2) \]ويمكن اعتبار كل مجموعة من هذه المجموعات في الاعتبار
\[\large x(x - 1) + 2(x - 1) \]والآن لدينا حدان لهما عامل مشترك \(x-1\) , لذا فنحن نعاملهما على أنهما
\[\large (x+2)(x - 1) \]أحيانًا يكون استخدام الآلة الحاسبة أكثر عملية لإيجاد العوامل. يمكنك استخدام ملفات حل المعادلات التربيعية لإيجاد عوامل التعبير التربيعي.
لاحظ أن هناك العديد من الأساليب التي يمكن أن تساعدك عندما تحتاج إلى تحليل تعبير , اعتمادًا على هيكله. واحد من هؤلاء هو طريقة عامل بالتجميع والتي , عندما تعمل , يمكن أن تبسط عملية التبسيط كثيرًا.