حل المعادلات لوغاريتمي
حل المعادلات اللوغارية هو شيء سيتعين عليك القيام به في كثير من الأحيان عند التعامل مع الإجراءات الجبرية, ويستحق تطوير استراتيجية ملموسة للتعامل معها.
ما ستعلمه في هذا البرنامج التعليمي هو الاستراتيجيات الرئيسية التي تحتاجها لمتابعة حل المعادلات اللوغارمية.
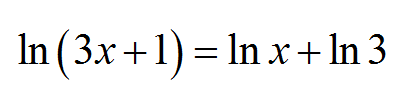
ما هي المعادلة اللوغارية؟
أول شيء نحتاج إليه هو تحديد ما هي معادلة لوغاريتمي.
المعادلة اللوغارمية هي معادلة تتضمن متغير واحد غير معروف واحد على الأقل, حيث يظهر تعبير لوغاريتمي على جانب واحد على الأقل من المعادلة
وبعد
مثال على معادلة لوغاريتمي
\[\ln x = 2\ln x - \ln 3\]أو أيضا
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
لاحظ أن معادلة لوغاريتمي يمكن أن تحتوي على أكثر من غير معروف, مثل على سبيل المثال
استراتيجيات لحل المعادلات لوغاريتمي
أول إخلاء المسؤول هو أنه لا توجد طرق مقاومة للرصاص لحل معادلة لوغاريتمي, ولا معادلة عامة لهذه المسألة.سبب ذلك هو كل الطرق تتحمل بنية معينة في المعادلة, وهذا ليس بالضرورة في جميع المعادلات.
لذلك, لا يمكننا إيجاد طريقة حل المعادلات اللوغارية, لأنه لا توجد طريقة واحدة ستعامل مع جميع الحالات الممكنة.
ومع ذلك, هناك بضعة استراتيجيات لمتابعة ذلك من شأنها أن تعطيك أفضل فرصة للذهاب إلى المعادلة وإيجاد حل, إذا كان هناك أحد.
أولا, حاول تجميع جميع التعبير اللوغاري في تعبير لوغاريتمي واحد.
يتم تحقيق ذلك عادة باستخدام أكثر شيوعا قواعد السجل , تتيح لك ضغط تعبير لوغاريتمي, إذا كان بنية التعبير يسمح بذلك بذلك.
ثانيا, بمجرد ضغط التعبيرات اللوغارمية قدر الإمكان, سوف تتخلص منها, من خلال تطبيق الوظيفة الأسية عادة على جانبي المساواة.
هذه الخطوة الأخيرة, نأمل أن تقوم بإزالة جميع اللوغاريثز من الصورة, وسوف تسمح لك بحلها من أجل المجهولين (غير المعروفين).
لذلك, بمعنى آخر, فإن حل معادلة لوغاريتمي يتكون من تجميع التعبيرات اللوغارمية, مما يلغيها عن طريق تطبيق الأسي, ثم حل المعادلة كمعادلة منتظمة.
من الواضح, عندما تتخلص من اللوغاريثز, فإنك تواجه أي معادلة يمكن أن يكون لها تحديات خاصة بها.
حل أمثلة مختلفة من المعادلات اللوغارمية
لا توجد طريقة أفضل في تعلم كيفية حل المعادلات من ممارسة فعلا حلها:
مثال 1:
حل المعادلة التالية:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]إجابه:
دعونا نتبع الاستراتيجيات.هذه الفكرة هي ضغط التعبيرات اللوغارمية قدر الإمكان.هذه هي دعوة الحكم, لأن الفكرة الرئيسية هي التخلص أساسا من اللوغاريتمي.
باستخدام قواعد السجل يمكننا وضع "4" داخل اللوغاريتم
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]الآن بعد أن تعبر التعبيرات اللوغارمية مضغوطة قدر الإمكان, نحتاج إلى التخلص من اللوغاريتمي.
طريقة واحدة للقيام بذلك هي تطبيق الدالة الأسية \(10^x\) لكل جانب من المساواة.ماذا أقصد بذلك ؟؟
حسنا, لديك وجهان في تلك المساواة.نظرا لأن كلا الجانبين هو نفسه, عند استخدامه كحجج لوظيفة \(10^x\), يجب أن يحافظ على المساواة.اذا لدينا
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]لأننا نعرف أن \(10^{\log a} = a\), وهو أحد قواعد السجل الأساسية.
حتى الآن لقد قمنا بالقضاء على اللوغاريتمي, يمكننا حل المعادلة المتبقية:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]لذلك ثم \(x_1 = 3 + 2\sqrt 2\) و \(x_2 = 3 - 2\sqrt 2\).من الناحية الفنية, تحتاج إلى التحقق مما إذا كانت هذه هي حلول المعادلة الأصلية, لذا تأكد من أنهم ينتمون إلى مجال التعبيرات اللوغارمية.
في هذه الحالة, كلاهما \(x_1 = 3 + 2\sqrt 2\) و \(x_2 = 3 - 2\sqrt 2\) هي حلول المعادلة الأصلية.
مثال 2:
حل المعادلة اللوغارية التالية:
\[\large \ln 5 - \ln(6-x) = \ln x\]إجابه:
باستخدام قواعد السجل, يمكننا ضغط تعبيرات السجل, ونحن نحصل على ذلك
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]لأننا نعرف أن \(e^{\ln a} = a\), وهو أحد قواعد السجل الأساسية.
لذلك, الآن بعد أن القضاء على اللوغاريثز, يمكننا حل المعادلة التي غادرناها:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]لذلك ثم \(x_1 = 1\) و \(x_2 = 5\).دعنا نقدم هذه القيم في المعادلة الأصلية لمعرفة ما إذا كانت في الواقع حلول:
ل \(x_1 = 1\):
وهو نفس:
\[\large \ln 5 - \ln(5) = 0\]وهذا صحيح, لذلك تعقد المعادلة.
ل \(x_1 = 5\):
وهو نفس:
\[\large \ln 5 - \ln(1) = \ln(5)\]وهذا صحيح, لذلك تعقد المعادلة.
لذلك, فإن الحلول للمعادلة هي \(x_1 = 1\) و \(x_2 = 5\).
المزيد عن حل المعادلات اللوغارية
شيء واحد يهتم الطلاب به هو كيف تتخلص من تسجيل الدخول إلى المعادلة.لكننا رأينا أن هذا هو في الواقع الجزء السهل.ما هو أصعب هو فعلا تعمل الجبري على التعبير بحيث يمكن إزالة السجلات.
هذا يطرح مسألة كيفية التعامل مع القواعد المختلفة, والتي تتطلب فقرة خاصة بها.
حل المعادلات اللوغارمية مع قواعد مختلفة
في الأمثلة أعلاه, نتعامل فقط مع \(\log\) (logarithm مع قاعدة 10) و \(\ln\) (اللوغاريتم مع قاعدة \(e\)).كيف يمكنك أن تفعل ذلك عندما يكون لديك لوغاريتم مع قاعدة مختلفة, مثل __xyz_d __ ؟؟
الجواب بسيط: من أجل القضاء على اللوغاريتمي مع قاعدة مختلفة, قل \(\log_a\) التي لديها قاعدة \(a\) نحن ببساطة استخدام الدالة الأسية \(a^x\).بسيط بسيط؟
في الواقع, القضاء على LOGARITHM هو الجزء السهل من حل معادلات السجل.الجزء الأكثر صعوبة من العملية هو تجميع وتعبيرات اللوغاريبمية المدمجة في شكل تقوم بإزالةها.
يمكنك معرفة المزيد حول كيفية عمل لوظيفة اللوغاريتمي من خلال الرؤية خصائص الرسم البياني لهي ودراسة قواعد السجل الأساسي وبعد