الجبر دروس

القضاء الغاوسي

إزالة Gaussian هي عملية يتم إجراؤها على مصفوفات تهدف إلى وضع مصفوفة فيها شكل القيادة . وجود مصفوفة بهذا الشكل يساعد بشكل كبير في حل معادلات المصفوفة بسهولة بالغة.

من الناحية الفنية , تتمثل عملية إجراء حذف Gaussian في العثور على عمود به محور (وهي اللغة العامية الفاخرة لعنصر غير صفري) تسمح لنا بإزالة جميع العناصر الموجودة أسفل المحور.

تتيح لنا عملية البحث عن المحاور والحذف وضع مصفوفة في شكل مستوى , والطريقة التي تسير بها العملية هي أنه من خلال التمحور , فإنك تضيف عمودًا جديدًا إلى نموذج المستوى , ولا `` تدمر '' المستوى الذي تشكله قد يصل إلى الخطوة السابقة. جميل إذا سألتني.

يصبح المصطلح "شكل المستوى" الذي تم الحصول عليه باستخدام إزالة Gaussian واضحًا من خلال النظر إلى المصفوفة أعلاه , حيث تحتوي العناصر غير الصفرية في المصفوفة على هيكل يشبه المستوى , كما هو موضح في الخط الأحمر.

الرياضيات وراء الاستبعاد المحوري والغاوسي

لن نتطرق إلى هذا الأمر بشكل تقني للغاية , سنحاول فقط أن تفهم الدافع والآليات الخاصة بهذا النوع من الإقصاء.

تكمن الفكرة في الحصول على مصفوفة \(A\) , ذات بُعد \(m \times n\) (وهي تحتوي على \(m\) صفوف وأعمدة \(n\)) في شكل مختلف يكون أكثر قابلية لحل المعادلات.

بشكل أكثر تحديدًا , بالنسبة لمصفوفة \(m\times n\) \(A\) , ومتجه \(m\times 1\) \(b\) , نحتاج إلى إيجاد متجه \(n\times 1\) \(x\) مثل ذلك

\[Ax = b\]

قد تعتقد , "هذا أمر سهل للغاية , نقوم فقط بضرب كل جانب في \(A^{-1}\) من اليسار" حتى نحصل على:

\[x = A^{-1} b \]

....ليس بهذه السرعة! هذا لا يعمل إلا عندما تكون المصفوفة \(A\) قابلة للعكس. للبدء , يجب أن تكون المصفوفة \(A\) عبارة عن مصفوفة مربعة , وبعد ذلك , يجب أن يكون محددها مختلفًا عن الصفر. لكن لا يمكنك الضرب في معكوس المصفوفات غير المربعة. لذا , كيف تفعل ذلك بعد ذلك؟

تحتاج إلى تحويل المعادلة إلى معادلة يسهل حلها.

على وجه التحديد , المصفوفات في شكل المستوى هي مصفوفات تؤدي إلى معادلات يسهل حلها (المزيد عن ذلك لاحقًا).

استخدام المصفوفات الأولية

بادئ ذي بدء , سوف نقدم ملاحظة حاسمة. إذا كان لدينا حل معادلة المصفوفة \(Ax = b\) , وكانت \(E\) مصفوفة قابلة للانعكاس , فإن \(x\) هي أيضًا حل \((EA)x = Eb\) , والعكس صحيح.

بمعنى آخر , معادلات المصفوفة

\[Ax = b\]

\[(EA)x = Eb\]

متكافئة , لمصفوفة معكوسة \(E\). ماذا نعني بأن المعادلات متكافئة؟ نعني أن المعادلات لها نفس الحلول.

إذن ما سنفعله هو أن نبدأ بـ \(Ax = b\) , وعن طريق الضرب في المصفوفات القابلة للعكس \(E\) , سنصل إلى معادلة مصفوفة مكافئة وهي أسهل بكثير في الحل .

لنفترض أننا قادرون على العثور على قائمة المصفوفات القابلة للعكس \(E_1, E_2, ..., E_n\) وضربنا (من اليسار) معادلة المصفوفة الأصلية لتحويلها إلى معادلة مكافئة , مثل:

\[Ax = b \,\,\,\, \Leftrightarrow \,\,\,\, (E_1 \cdot A)x = (E_1 \cdot b)\] \[... \Leftrightarrow \,\,\,\, (E_n \cdots E_2 \cdot E_1 \cdot A)x = (E_n \cdots E_2 \cdot E_1 \cdot b)\] \[ \Leftrightarrow \,\,\,\, \tilde A x = \tilde b\]

حيث \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) و \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\).

هدفنا هو بعناية يختار المصفوفات القابلة للعكس \(E_1, E_2, ..., E_n\) بحيث تكون \(\tilde A\) في شكل المستوى.

لماذا هذا؟ لأنه إذا كان \(\tilde A\) في شكل تسلسل , فإن حل معادلة المصفوفة \(\tilde A x = \tilde b\) يكون أسهل بكثير , ونحن نعلم بالفعل أن \(\tilde A x = \tilde b\) له نفس الحلول مثل \(A x = b\)

مثال 1

دعونا نرى لماذا يكون حل معادلة مصفوفة أسهل بكثير عندما يكون لديك في صيغة القيادة. تخيل أولاً أن لديك المصفوفة والمتجه التاليين:

\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & -1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]

وتريد حل \(Ax = b\). كيف سيبدو نظام المعادلات؟ سيبدو النظام \(Ax = b\)

\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 - x_3 = 1\]

كيف تبدو؟ حسنًا , ليس هذا أنيقًا. سوف تحتاج إلى بدء حل المعادلات. هناك طرق منهجية إلى حد ما لحل هذه المشكلة باستخدام أشياء مثل الحذف وما إلى ذلك , لكنها على الأقل مرهقة.

الآن , من ناحية أخرى , تخيل أن لديك المصفوفة والمتجه التاليين:

\[\tilde A = \left[ \begin{matrix} -1 & 1 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{matrix} \right] \] \[\tilde b= \left[ \begin{matrix} 1 \\ -1 \\ -1 \\ \end{matrix} \right]\]

وتريد حل \(\tilde A x = \tilde b\). في هذه الحالة , تكون المصفوفة \(\tilde A\) في شكل متسلسل. كيف سيبدو نظام المعادلات؟ سيبدو النظام \(\tilde A x = \tilde b\)

\[-x_1 + x_2 + x_3 = 1\] \[x_2 - x_3 = -1\] \[x_3 = -1\]

كيف تبدو هذه؟ حسنًا , ليس رثًا جدًا.

في الواقع , إذا بدأنا مباشرة من المعادلة الثالثة , لدينا \(x_3 = -1\) مباشرة. ثم من المعادلة الثانية \(x_2 = -1 + x_3 = -1 + (-1) = -2\). ومن المعادلة الأولى \(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\). لذلك بدون أي ضباب وجدنا ما يلي:

\[x_1 = -4, \, x_2 = -2, x_3 = -1\]

لذلك , في هذه الحالة يتم حل النظام بشكل تافه.

بالنسبة للأنظمة المرتبطة بالمصفوفات في شكل المستوى , من السهل التراجع عن المعادلة الأخيرة إلى المعادلة الأولى , للحصول على الحلول.

كيفية اختيار المصفوفات الصحيحة المعكوسة

الآن بعد أن علمنا أن العمل مع المصفوفات في شكل المستوى يجعل من السهل جدًا حل معادلات المصفوفات , يجب أن نتساءل , ما هي المصفوفات القابلة للعكس \(E_1, E_2, ..., E_n\) التي ستجعل \(\tilde A\) في شكل المستوى.

كيف يعمل القضاء على Gaussian؟

ومن المثير للاهتمام أنه ليس من الصعب العثور على هذه المصفوفات \(E_1, E_2, ..., E_n\) , والتي ستسمى المصفوفات الأولية.

الخطوة 1 : انظر إلى العمود الأول , إذا كان يحتوي على قيمة غير صفرية , فسيكون هذا هو المحور الخاص بك. إذا كان الصف الأول من العمود الأول غير صفري , فاستخدمه كمحور. إذا لم يكن الأمر كذلك , فابحث عن صف له قيمة غير صفرية وتبديل هذا الصف والصف الأول.

لذلك , تجد محورًا , وربما تحتاج إلى إجراء تبديل للصفوف (والذي يتم تمثيله بالفعل بضربه في مصفوفة معينة قابلة للانعكاس)

الخطوة 2 : بمجرد أن يكون لديك المحور , قم بإزالة جميع العناصر الموجودة في العمود الحالي , أسفل المحور.

يتم ذلك بضرب الصف المحوري في ثابت معين , وإضافة ذلك إلى صف أسفل المحور , بحيث يصبح العنصر الموجود في نفس العمود مثل المحور صفرًا.

الخطوه 3 : بمجرد جعل جميع العناصر الموجودة أسفل المحور صفراً عن طريق إجراء عمليات الصف المناسبة (والتي يتم تمثيلها من خلال تشغيل مصفوفة قابلة للانعكاس) , انتقل إلى العمود التالي , الصف التالي , وابحث عن المحور من الصف أدناه من صف المحور السابق وقم بإجراء نفس الإجراء.

الخطوة 4 : كرر حتى تنفد الأعمدة أو تصبح المصفوفة في شكل متسلسل.

مثال 2

حل النظام التالي باستخدام نظام التمحور والقضاء الغاوسي:

\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 + x_3 = 1\]

إجابه:

أولاً وقبل كل شيء , المصفوفة المرتبطة \(A\) والمتجه \(b\) هي:

\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & 1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]

المصفوفة المعززة \([A|b]\) هي

\[\left[ \begin{matrix} 1 & 1 & 1 & 2 \\ 1 & -1 & 1 & 1 \\ -1 & 1 & 1 & 1 \\ \end{matrix} \right]\]

من أجل حل النظام , علينا أن نذهب للحذف الغاوسي. نختار المحور الأول , بدءًا من العمود الأول. العنصر الموجود في الصف الأول من العمود الأول هو 1 , والذي يختلف عن الصفر , ثم يتم استخدامه كمحور. نستخدم هذا المحور (1) لإزالة جميع العناصر الموجودة أسفله:

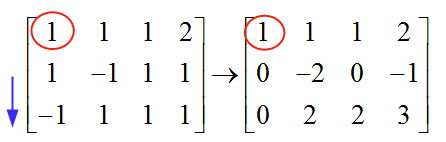
آلية إزالة العناصر الموجودة أسفل المحور بسيطة. في هذه الحالة , لحذف الرقم "1" الموجود أسفل المحور , أطرح العناصر الموجودة في الصف 1 إلى العناصر الموجودة في الصف 2. وبهذه الطريقة سأكوّن صفرًا أسفل المحور.

وبالمثل , لاستبعاد "-1" الموجود في الصف 3 , أقوم بإضافة العناصر الموجودة في الصف 1 إلى العناصر الموجودة في الصف 3. وبهذه الطريقة أقوم بتكوين صفر تحت المحور في الصف 3.

سنرى أن عمليات السطر هذه تتحقق عن طريق الضرب في مصفوفة عكسية , لذلك لدينا أنظمة مكافئة من خلال القيام بذلك.

الآن , بالانتقال إلى الصف التالي , العمود التالي , نجد "-2" , والذي يختلف عن الصفر , وبالتالي , يتم استخدامه كمحور. لإزالة القيمة الموجودة أسفل هذا المحور , نضيف إلى الصف 3 قيم الصف 2:

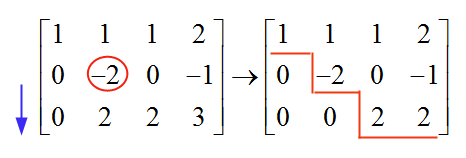
والآن نتوقف , لأن المصفوفة الناتجة هي بالفعل في شكل رتبة. نحن الآن نعود إلى الوراء لحل النظام:

\[2x_3 = 2 \,\,\,\, \Rightarrow \,\,\,\, x_3 = 1\] \[-2x_2 = -1 \,\,\,\, \Rightarrow \,\,\,\, x_2 = 1/2\] \[x_1+x_2+x_3 = 1 \,\,\,\, \Rightarrow \,\,\,\, x_1 = 1 - x_2 - x_3 = 1 - 1/2 - 1 = -1/2\]