قاعدة كرامر
قاعدة كرامر هي تقنية تستخدم لحل أنظمة المعادلات الخطية بشكل منهجي , بناءً على حسابات المحددات.
عادة , حل أنظمة المعادلات الخطية يمكن أن يكون فوضويًا للأنظمة الأكبر من 2 × 2 , نظرًا لوجود العديد من الطرق لتقليلها عند وجود ثلاثة متغيرات أو أكثر.
توفر قاعدة كرامر طريقة منهجية لا لبس فيها لإيجاد حلول لأنظمة المعادلات الخطية , بغض النظر عن حجم النظام.
يزيد عدد الحسابات المطلوبة للأنظمة الكبيرة , لكن الإجراء هو نفسه تمامًا , بغض النظر عن حجم النظام.
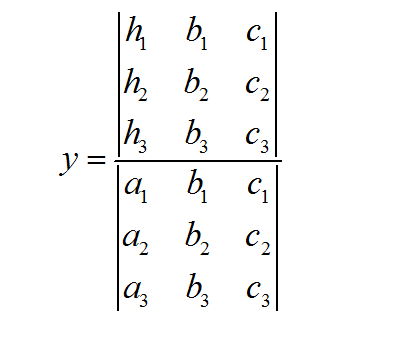
كيفية استخدام قاعدة كرامر
من أجل تسهيل الأمور , سنعمل على حل قضية \(n = 2\) وبعد ذلك سننشئ نسخة أكثر عمومية والتي نأمل أن تكون منطقية بشكل أفضل بعد معالجة قضية \(n=2\).
الخطوة 1
: يمكن كتابة جميع الأنظمة الخطية 2x2 بالشكل التالي:
إذن خطوتك الأولى هي إيجاد هاتين القيمتين \(a_1, b_1, c_1\) و \(a_2, b_2, c_2\) للنظام الذي تريد حله.
الخطوة 2
: بمجرد حصولك على المعاملين \(a_1, b_1, c_1\) و \(a_2, b_2, c_2\) , تستخدم الصيغ التالية لحل المعاملين \(x\) و \(y\):
في الصيغة أعلاه , حيث تقول "det" , فهذا يعني محدد المصفوفة المقابلة. في بعض الأحيان , يتم استخدام تدوين أكثر إحكاما للمحددات , كما هو موضح أدناه:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]لذلك , باستخدام الترميز أعلاه , سنحصل على هذه الصيغ الأكثر إحكاما لقاعدة كرامر:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]دعونا نمتلك طريقة بصرية لفهم ما يحدث. لاحظ أن كلاً من \(x\) و \(y\) لهما نفس المحدد في المقام.
تُشتق معاملات تلك المصفوفة المشتركة المستخدمة في المقام مباشرة من المعاملات التي تضرب \(x\) و \(y\) في النظام. انظر الصورة أدناه:
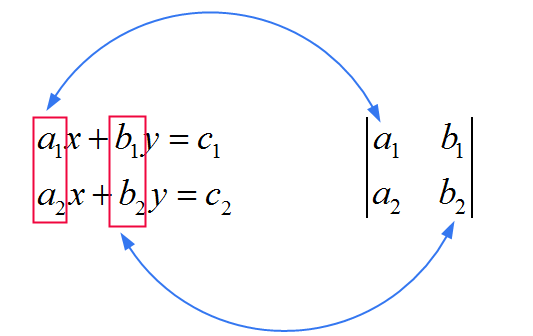
الآن نرى أن \(x\) و \(y\) يختلفان فيما بينهما في البسط. كطريقة لتذكر القاعدة , فكر في هذا:
بالنسبة إلى \(x\) , يمكنك استخدام نفس المصفوفة باعتبارها المصفوفة الموجودة في المقام , فقط أنك تستبدل العمود الأول بالمعاملات \(c_1\) و \(c_2\). انظر الصورة أدناه
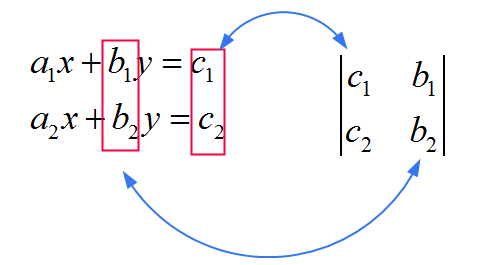
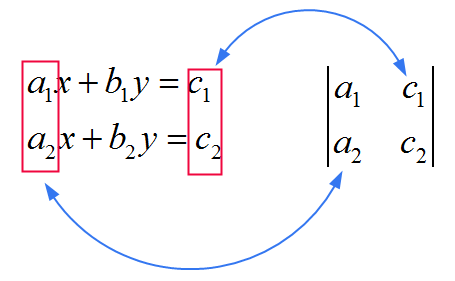
بالنسبة إلى \(y\) , يمكنك استخدام مصفوفة SAME باعتبارها المصفوفة الموجودة في المقام , فقط لاستبدال العمود الثاني بالمعاملات \(c_1\) و \(c_2\). انظر الصورة أدناه
مثال 1
حل النظام الخطي 2 × 2 التالي:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]إجابه:
دعونا نتبع الخطوتين اللتين حددناهما أعلاه لاستخدام قاعدة كرامر لحل النظام أعلاه:
الخطوة 1
: نحتاج إلى تحديد معاملات المحددات المقابلة.
نستخدم للمصفوفة الموجودة في المقام
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]الآن , في هذه الحالة \(c_1 = 10, c_2 = 4\) , للمحدد المستخدم لحساب \(x\) , نستبدل المصفوفة السابقة بتغيير العمود الأول:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]بالنسبة للمحدد المستخدم لحساب \(y\) , فإننا نستبدل المصفوفة السابقة بتغيير العمود الثاني:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]الآن نحصل على الحل:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]و \(y\):
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]لذلك , الحل هو \(x = 3\) , \(y = 1/2\).
قاعدة كرامر للقضية العامة
يكمن جمال قاعدة كرامر في أنها تطبق نفس الإجراء تمامًا , سواء كان نظامًا 2 × 2 أو إذا كان نظامًا 10 × 10. المفهوم هو نفسه.
لذلك , افترض أن \(x_1, x_2, ..., x_n\) هي المتغيرات (المجهول) , ونريد حل نظام nxn التالي للمعادلات الخطية:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]لحل مشكلة \(x_1, x_2, ..., x_n\) , سنستخدم المحدد التالي في المقام:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• الحل لـ \(x_1\) هو
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• الحل لـ \(x_2\) هو
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]وما إلى ذلك وهلم جرا. كما ترى , المحدد في المقام هو نفسه , ويتم الحصول على المحدد في البسط بتغيير العمود الأول بـ \((c_1, ..., c_n)\) لـ \(x_1\). بالنسبة إلى \(x_2\) نقوم بتغيير العمود الثاني بمقدار \((c_1, ..., c_n)\) , بالنسبة إلى \(x_3\) نقوم بتغيير العمود الثالث , وهكذا. انت وجدت الفكرة.
مثال 2
حل نظام المعادلات الخطية التالية 3 × 3 باستخدام قاعدة كرامر.
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]إجابه:
بادئ ذي بدء , نحدد المحدد الموجود في المقام:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]نحتاج أيضًا إلى تحديد متجه معاملات \(c_i\):
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]سيكون هذا المتجه هو الذي سيحل محل الأعمدة المقابلة للمُحدد المشترك من المقام. نحن نحصل:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]المزيد عن قاعدة كرامر
قاعدة كرامر لها دور محدد في حل أنظمة المعادلات الخطية بكفاءة. إنه ينطوي على استخدام المحددات لجعل مهمة مباشرة للغاية والتي لولا ذلك ستكون معقدة حقًا , خاصة بالنسبة للأنظمة الأكبر.
في النهاية , من أجل حل الأنظمة الخطية , كل ما عليك فعله هو تحديد محددات مصفوفة الأرقام بناءً على النظام الذي يحتاج إلى حل , وإجراء عملية جبرية بسيطة لحل النظام.
التطبيقات
قاعدة كرامر لها العديد من التطبيقات في كل من الجبر الخطي والمعادلات التفاضلية.