الجبر دروس

مقاربة أفقية

في هذا البرنامج التعليمي سوف نغطي مفهوم Mقaarbة أفقyة وأهم تطبيقاتها.سنحاول تجنب أي تفسيرات تقنية مفرطة , ولكن سيتم استخدام بعض لمسات حساب التفاضل والتكامل.

في الغالب , فإن الجزء المهم للخروج من هذا البرنامج التعليمي هو حدس هندسي قوي حول التقارب الأفقي.هيا نبدأ!

ما هو المقاربة الأفقية

المقاربة الأفقية هي الحد الأعلى , يمكنك تخيله كخط أفقي يحدد حد لسلوك الرسم البياني لوظيفة معينة.

هذا يعني أن الرسم البياني للدالة \(f(x)\) نوع من الأساليب لهذا الخط الأفقي , مع زيادة قيمة \(x\).

كيف تجد مقاربًا أفقيًا؟

إن فهم هذا السلوك الأفقي للوظائف التي تظهر هذه الخاصية يمكن أن يكون مفيدًا جدًا لإيجاد تقارب أفقي.

في الواقع , في ظروف معينة , يشبه هذا السلوك المحد إلى حد كبير خيط خط أفقي للقيم الكبيرة من \(x\).انظر الوظيفة أدناه على سبيل المثال.

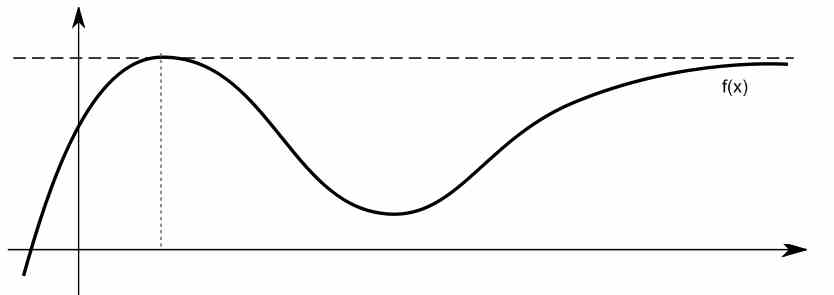
كيف تجد مقاربًا أفقيًا للوظيفة باستخدام حدود؟

من أجل توضيح التعريف , فإن الخط الأفقي \(y = h\) هو مقارب أفقي للوظيفة \(f(x)\)

\[\large \lim_{x\to\infty} f(x) = h\]

إذا كان الحد المذكور أعلاه موجودًا وهو محدود.بالنسبة لأولئك الذين لم يمروا بعد من خلال فئة حساب التفاضل والتكامل , فإن الخط الأفقي \(y = h\) هو مقارب أفقي للوظيفة \(f(x)\) عندما يكون \(h\) هو ود من \(f(x)\) كـ \(x\) يقترب من اللانهاية.ماذا يعني كونك "الحد"؟وهذا يعني أنه بالنسبة للقيم كبيرة بما فيه الكفاية من \(x\), ستكون قيمة \(f(x)\)أقرب إلى \(h\)كما نحن محددة مسبقًا.يتوهم , أليس كذلك؟

ما هي الصيغة لخلاف الأفقي؟

من أجل العثور على الصيغة لتقارب أفقي , نحتاج أولاً إلى العثور على الحد المقابل.افترض أن لديك

\[\large \lim_{x\to\infty} f(x) = h\]

في هذه الحالة , سوف نقول أن المقاربة الأفق هو \(h\), وصيغة التقارب الأفقي هي \(y = h\).وبعبارة أخرى , فإن المقاربة الأفقية بسيطة هو الخط الأفقي , وهذا هو خط مع Slope Zero.

هذا يعطي المعنى إلى ما يعنيه المقارب الأفقي من حيث الحدود: الحد الأقصى الموجود يتوافق مع تحديد الخط الأفقي الذي يسمى مقارب أفقي.

مثال 1

ابحث عن مقاربة أفقية للوظيفة

\[ \large f(x) = \frac{x^2}{x^2+1} \]

إجابه:

من أجل العثور على مقارب أفقي , نحتاج إلى العثور على الحد من الوظيفة \(f(x)\) كقاربة \(x\) إلى Infinity.إذا لم تكن معتادًا على حساب التفاضل والتكامل , فيجب عليك أولاً محاولة تقييم الوظيفة بقيمة كبيرة جدًا من \(x\).

على سبيل المثال , دعنا نقول أن \(x = 1,000,000\).دعنا نقوم بتوصيل هذا الرقم في الوظيفة:

\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]

وهو ما يقترب من 1. لذلك ينبغي للمرء أن يشك في أن الحد هو 1. في الواقع , اتضح أنه عندما تكون \(x\)كبيرة , فإن قيمة \(x^2\)كبيرة جدًا فيما يتعلق بـ 1 , بحيث \(x^2\)يشبه إلى حد كبير \(x^2 + 1\) على الأقل من الناحية النسبية.لذلك لدينا , من خلال تقسيم البسط والمقام بواسطة \(x^2\):

\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]

لأن \(\frac{1}{x^2}\) يقترب إلى 0 مع اقتراب \(x\) من Infinity.لذلك , ليس من الصعب إثبات ذلك , أو أن تكون مقتنعًا بذلك

\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]

مما يعني أن المقاربة الأفقية هي \(y = 1\).الآن , كن حذرًا من إجابتك إذا كنت تجيب على اختبار أو واجبات منزلية.سيقول بعض الناس "عدم التقارب الأفقي هو 1" , وهو أمر خاطئ.

من الناحية الفنية , فإن المقارب الأفقي هو الوظيفة \(y = 1\), وليس الرقم 1. إن المقاربة الأفقية هي وظيفة ثابتة , وهي ليست هي نفسها.مجرد قول , لأن هناك بعض طلاب الصف صعب الإرضاء هناك.

مثال 2

ابحث عن مقاربة أفقية , إذا كان موجودًا للوظيفة

\[ \large f(x) = \frac{x^3}{x^2+1} \]

إجابه:

بتقسيم البسط والمقام على \(x^2\):

\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]

لكن انتظر!الخدعة لم تعمل هنا؟نعم فعلت.لاحظ أن المقام سيصبح قريبًا جدًا من 1 لأن \(x\) يصبح كبيرًا جدًا , وسيصبح البسط كبيرًا جدًا.

ليس من الصعب تصديق أن \(f(x)\) يتقارب مع اللانهاية , بحيث لا يوجد مقارب أفقي.في أي وقت نرى فيه وظيفة غير محدودة , كما هو الحال بالنسبة لـ \(f(x)\) في هذا المثال , لن يكون لدينا مقارب أفقي.

مقارب أفقي أو تقارب أفقي؟

من الناحية الفنية , يمكن أن يكون هناك اثنين من التقارب الأفقي , واحد إلى اليسار وواحد إلى اليمين.المقاربة الأفقية اليسرى هي \(y = h_L\) إذا

\[\large \lim_{x \to -\infty} f(x) = h_L\]

وبالمثل , فإن المقاربة الأفقية اليمنى هي \(y = h_R\)

\[\large \lim_{x \to +\infty} f(x) = h_R\]

في حالة وجود أي من الحدود المذكورة أعلاه , ومحدودة.يمكن أن يحدث أن يكون للوظيفة تقاربان أفقيان , فهي تحتوي على مقارب واحد أفقي واحد فقط , أو لا تحتوي على أي شيء.

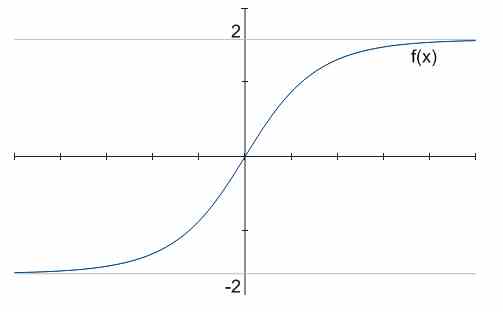
على سبيل المثال , في الرسم البياني أعلاه , هناك نوعان من التقارب الأفقي , \(y = -2\)و \(y = 2\).

ما هي قاعدة إيجاد مقاربة أفقية؟

لا توجد قواعد عامة ستعمل لجميع الحالات.في الحالة العامة , نحتاج إلى حساب الحد مع اقتراب \(x\)إلى \(-\infty\), والحد من \(x\)يقترب من \(+\infty\).

في حالة وجود أي من هذه الحدود ومحدودة , سيكون لدينا تقارب أفقي.

يمكن وضع إحدى القواعد المحددة للحالة أن الوظيفة المعطاة \(f(x)\) هي حاصل على تعبئتين.إذا كانت هذه هي الحالة , فلنفترض أن \(m\) هو ترتيب الحدود في البسط , و \(n\) هو ترتيب متعدد الحدود في المقام.ثم لدينا الحالات التالية:

شال 1: إذا كان \(m < n\), فإن التقارب الأفقي هو \(y = 0\).

الله 2: إذا كان \(m = n\), و \(a\)هو المعامل الرائد للعديد من الحدود في البسط , و \(b\)هو المعامل الرائد للعديد من الحدود في المقامس , فإن عدم التقارب الأفقي هو \(\displaystyle y = \frac{a}{b}\).

alحaitlة 3: إذا كان \(m > n\), فلا يوجد مقارب أفقي.

مثال 2

ابحث , إذا كانت موجودة , مقاربة أفقية للوظيفة

\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]

إجابه:

تتكون الوظيفة من حاصل اثنين من الحدود.كثير الحدود في البسط هو \(3x^2+2x-1\), وهو متعدد الحدود من الطلب 2 , إذن ثم \(m = 2\), والمعاملات الرائدة 3.

كثير الحدود في المقامس هو \(2x^2 -x+2\), وهو متعدد الحدود من الطلب 2 , ثم \(n = 2\), وقيادة ثابت 2. يمكنك استخدامنا حASBة alحdod الهادود لإجراء هذا القسم الذي يوضح جميع الخطوات.

وبالتالي , لأنه في هذه الحالة \(m = n\), هناك مقاربة أفقية , وهي حاصل على المعاملات الرائدة , لذلك في هذه الحالة , يكون التقارب الأفقي هو

\[\large y = \frac{3}{2}\]