日志规则
对数函数是数学中最重要的函数之一,对数规则简单方便,让对数的处理变得非常容易。
让我们先回忆一下 \(\log_b a\) 是什么意思。在这种情况下,值 \(b\) 是 根据 的对数,而 \(a\) 是 争论 .
当 \(b^y = a\) 时,我们说 \(\log_b a = y\)。这就是说 \(\log_b a\) 是 \(b\)(基数)需要提高到以获得 \(a\)(参数)的数字。
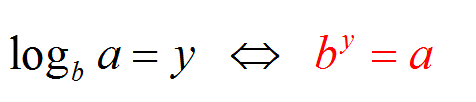
例如,\(\log_{10} 25\) 对应于我需要将 10 提高到 25 的数字。所以我正在寻找的对数是具有 \(10^y = 25\) 属性的数字 \(y\)
现在的问题是,我们如何计算具有 \(10^y = 25\) 属性的数字 \(y\)?嗯,这个数字是明确定义的,对数函数 \(f(x) = \log_{10} x\) 会处理它。这个函数不是初等函数,需要用泰勒级数(无穷级数)来表示。
或者,您可以使用计算器(这可能更容易,对吧?)。
对数规则:对数的性质
这些是主要的日志规则:
规则1 :\(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
规则#2 :\(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
规则#3 :\(\large \log_a (b^c) = c \cdot \log_a (b) \)
规则#4 :\(\large \log_a (a) = 1 \)
规则#5 :\(\large \log_a (1) = 0 \)
示例 1
使用日志规则简化 \(\log_2 8 + \log_2 4\):
回答:
使用规则#1,我们发现:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]所以,第一步是规则#1 的简单应用,但我们如何得到\(\log_2 32 = 5\)?这是因为\(2^5 = 32\),所以在这种情况下,我们直接找到你需要提高\(2\)的数字是多少才能得到\(32\)。
大多数对数你需要一个计算器来计算它们。只有少数几个可以直接计算。像 \(\log_{10} 100 = 2\) 这样的东西,因为你很容易知道 \(10^2 = 100\)。
但是,你能直接计算 \(\log_{10} 102\) 吗?不是真的,你需要一个计算器。
示例 2
表达对数的和和减法:\( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \)。
回答:
首先,我们需要记住,取三次方是 \(1/3\) 次方。换句话说,\(\sqrt[3]{x}\) 与 \(x^{1/3}\) 相同。
那么,我们首先使用规则#3 将幂放在对数前面,然后我们使用规则#1 和#2。我们得到:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]这就是所需要的:简单对数的求和和减法。
对数基公式的变化
与对数相关的最有用的公式之一是基数公式的变化。这个公式是这样的:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]这个公式只是说,如果要将基数从\(b\)改为\(c\),结果本质上是一样的,只是需要除以新基数的对数。
现在,如果您以艺术为导向,您可能会喜欢下面表达的基础公式变化的替代形式:
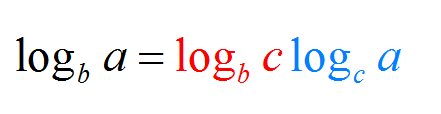
示例 3
用 \(\log\)(以 10 为底)表示自然对数 \(\ln\)。
回答:
使用基本公式的变化,我们得到:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]所以你是说 \(\ln a\) 是通过将 \(\log a\) 除以 \(\log e\) 得到的。多方便?谁说数学很难?
更多关于日志规则
对数在数学中非常重要。从历史上看,对数在天文学中扮演着非常重要的角色,作为预测月球和行星运动的一种方式。
对数函数是数学中一切事物的中心,它与指数,指数和几乎所有事物交织在一起。这就是为什么他们要求你背诵对数,因为它们很重要。
此外,此处介绍的这些日志规则在促进 对数方程的解析 .
符号约定
您需要了解一些符号约定。一般来说,我们写 \(\log_b a\),我们称它为“a 的对数基数 b”。当基数是 \(b = 10\) 时,按照惯例我们只写 \(\log a\)。因此,当您看到没有基数的 \(\log\) 时,假定基数是 \(10\)。
还有一个值得注意的案例。对于 \(\log_b a\),当基数是 \(b = e\)(欧拉常数)时,我们写 \(\ln a\) 而不是 \(\log_e a\)。因此,当使用 \(\ln\) 代替 \(\log\) 时,是因为对数的底是 \(e\)。
观察到 \(\ln a\) 通常被称为 自然对数 .是的,自然日志与一般日志具有相同的规则。
如果您想绘制对数函数,可以尝试我们的 对数函数图制作器 ,这将为您提供一个整齐呈现的图表。
