水平渐近线
在本教程中,我们将介绍 水平渐近线 及其最重要的应用。我们将尽量避免过于技术性的解释,但也会用到微积分的一些知识。
从本教程中获得的最重要的部分是关于水平渐近线的强烈几何直觉。让我们开始吧!
什么是水平渐近线
水平渐近线是一个上限,可以把它想象成一条水平线,它为给定函数的图形行为设定了一个界限。
这意味着,随着 \(x\) 值的增加,函数 \(f(x)\) 的图形有点接近这条水平线。
如何找到水平渐近线?
了解表现出这一特征的函数的这种极限水平行为,对于找到水平渐近线非常有用。
事实上,在某些情况下,当 \(x\) 的值较大时,这种限制行为看起来很像一条水平线。请看下面的函数示例。
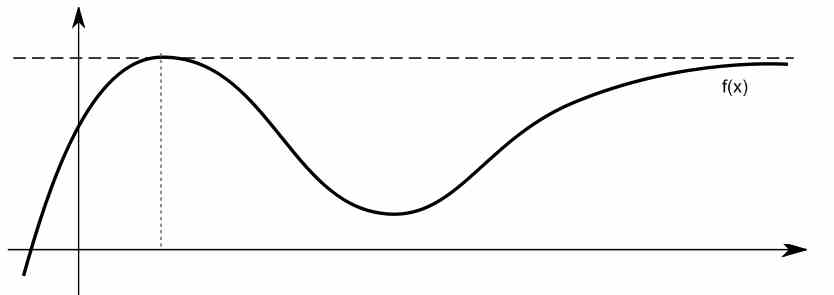
如何利用极限找到函数的水平渐近线?
为了使定义更加清晰,在下列情况下,水平线 \(y = h\) 是函数 \(f(x)\) 的水平渐近线
\[\large \lim_{x\to\infty} f(x) = h\]如果存在上述极限并且它是有限的。对于那些还没有上过微积分课的人来说,当 \(h\) 是函数 \(f(x)\) 的水平渐近线时,水平线 \(y = h\) 是函数 \(f(x)\) 的水平渐近线。 易腐烂 的 \(f(x)\) 接近无穷大。极限 "意味着什么?它意味着对于足够大的 \(x\) 值,\(f(x)\) 的值将与我们预先确定的 \(h\) 一样接近。很有意思吧?
水平渐近线的公式是什么?
为了找到水平渐近线的公式,我们首先需要找到相应的极限。假设
\[\large \lim_{x\to\infty} f(x) = h\]在这种情况下,我们会说水平渐近线是 \(h\),水平渐近线的公式是 \(y = h\)。换句话说,水平渐近线就是简单的水平直线,这是一条斜率为零的直线。
这就给出了水平渐近线在极限方面的含义:找到的极限对应于定义水平线,即水平渐近线。
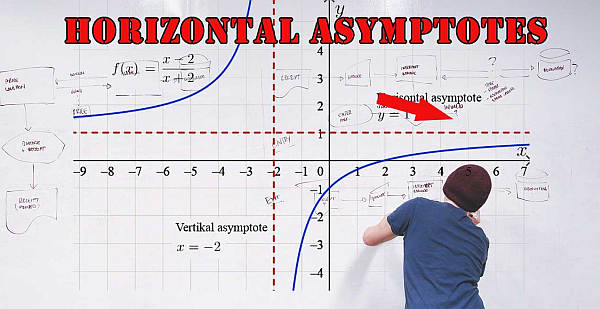
实例1
求函数的水平渐近线
\[ \large f(x) = \frac{x^2}{x^2+1} \]回答:
为了找到水平渐近线,我们需要找到当 \(x\) 接近无穷大时函数 \(f(x)\) 的极限。如果您不熟悉微积分,则应首先尝试在 \(x\) 的很大值上对函数进行求值。
例如,假设 \(x = 1,000,000\)。让我们把这个数字输入函数:
\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]事实上,当 \(x\) 较大时,\(x^2\) 的值相对于 1 而言非常大,以至于 \(x^2\) 至少相对于 \(x^2 + 1\) 非常相似。因此,用 \(x^2\) 除以分子和分母,我们可以得出
\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]因为 \(\frac{1}{x^2}\) 接近 0 时,\(x\) 接近无穷大。因此,不难证明或确信
\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]这意味着水平渐近线是 \(y = 1\)。现在,如果你在考试或家庭作业中作答,请注意你的答案。有些人会说 "水平渐近线是 1",这是错误的。
严格来说,水平渐近线是函数 \(y = 1\),而不是数字 1。水平渐近线是一个恒定的函数,与数字不同。我只是说说而已,因为有些学生很挑剔。
示例 2
为函数找出水平渐近线(如果存在的话
\[ \large f(x) = \frac{x^3}{x^2+1} \]回答:
用 \(x^2\) 除以分子和分母:
\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]但是,等等!这招在这里不管用?是的,起作用了。请注意,当 \(x\) 变大时,分母会变得非常接近 1,而分子也会变得非常大。
我们不难相信 \(f(x)\) 收敛到无穷大,因此不存在水平渐近线。任何时候我们看到的函数都是无边界的,就像本例中的 \(f(x)\),我们不会看到水平渐近线。
水平渐近线还是水平渐近线?
从技术上讲,可能有两条水平渐近线,一条向左,一条向右。左边的水平渐近线是 \(y = h_L\),如果
\[\large \lim_{x \to -\infty} f(x) = h_L\]同样,右水平渐近线为 \(y = h_R\) ,如果
\[\large \lim_{x \to +\infty} f(x) = h_R\]如果存在上述任何一个极限,并且是有限的。一个函数可能有两个水平渐近线,也可能只有一个水平渐近线,或者没有。
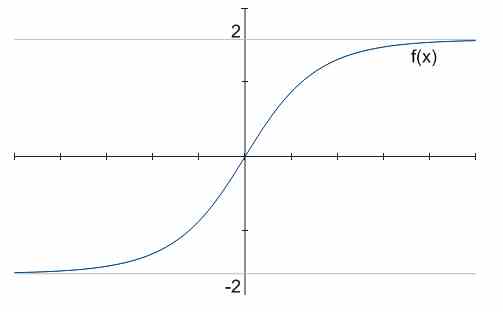
例如,在上图中,有两个水平渐近线,分别是 \(y = -2\) 和 \(y = 2\)。
求水平渐近线的规则是什么?
没有适用于所有情况的通用规则。在一般情况下,我们需要计算 \(x\) 接近 \(-\infty\) 时的极限,以及 \(x\) 接近 \(+\infty\) 时的极限。
如果其中任何一个极限存在并且是有限的,我们就会得到水平渐近线。
在给定函数 \(f(x)\) 是两个多项式的商的情况下,可以设计出一条特定的规则。如果是这种情况,让我们假设 \(m\) 是分子中多项式的阶,而 \(n\) 是分母中多项式的阶。那么我们有以下几种情况:
案例 1: 如果 \(m < n\),那么水平渐近线就是 \(y = 0\)。
案例 2: 如果 \(m = n\),而 \(a\) 是分子中多项式的前导系数,\(b\) 是分母中多项式的前导系数,那么水平渐近线就是 \(\displaystyle y = \frac{a}{b}\)。
案例 3: 如果 \(m > n\),则不存在水平渐近线。
示例 2
如果存在,找出函数的水平渐近线
\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]回答:
该函数由两个多项式的商组成。分子中的多项式是 \(3x^2+2x-1\),它是阶数为 2 的多项式,那么 \(m = 2\),前导系数为 3。
分母中的多项式是 \(2x^2 -x+2\),它是 2 阶多项式,所以是 \(n = 2\),前导常数是 2。您可以使用我们的 多项式计算器 进行分部,显示所有步骤。
因此,由于在这种情况下 \(m = n\),有一个水平渐近线,它是前导系数的商,所以在这种情况下,水平渐近线是
\[\large y = \frac{3}{2}\]关于水平渐近线的更多信息
你的问题是如何找到方程的渐近线,对吗?首先,你要找到一个 功能 而不是方程。那么,你需要从一般定义入手,使用极限。
如果你不懂微积分,也不知道如何计算极限,那么你至少应该尝试在函数上插入非常大的 \(x\)值,以及非常负的 \(x\)值,看看函数的表现如何。
如果存在水平渐近线,即使使用某些软件绘制函数图,也能给出明确的提示。
最终,在非常有限的情况下,函数是一个 多项式商 然后,您就可以根据订单 \(m\) 和 \(n\) 应用该规则。
如何找到不同度数的水平渐近线?
这些是不同类型的渐近线,它们被称为斜渐近线。我们将在另一个教程中讨论斜渐近线。
