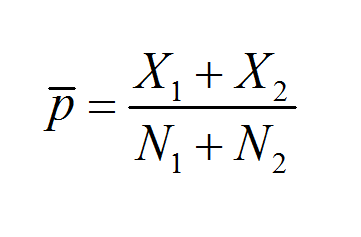比例计算器

此计算器可帮助您计算比例关系 A / B = C / D,您需要提供四个数值表达式中的三个来找到缺失的那个。您也可以提供所有四个,在这种情况下,计算器将评估比例是否适用于提供的数字。

一旦您提供了所需的数值表达式（可以是数字或任何有效的数值表达式）,您就可以单击"计算"按钮来显示计算结果。

如何使用此比例计算器？

使用此比例计算器将简化您解决数学比例的过程。以下是您应该遵循的步骤：

• 确定比例： 确定需要计算的比例
• 输入已知值： 将已知值输入到提供的框中,您需要比例涉及的四个数字中的三个数字。
• 计算： 点击计算按钮获取结果。计算器将显示缺失的值。

解决比例的步骤

以下是手动解决比例的方法：

• 设置比例： 以分数形式写出比率,如\(\frac{A}{B} = \frac{C}{D}\)。
• 交叉相乘： 将第一个分数的分子乘以第二个分数的分母,反之亦然：\(A \times D = B \times C\)。
• 求解未知数： 如果您正在求解\(x\),请重新排列方程以分离\(x\)。
• 检查你的工作： 将找到的值代入原始比例,确保比例相等。

比例公式解释

比例的基本公式是：

\[ \frac{A}{B} = \frac{C}{D} \]

其中 \(A\) 和 \(B\) 是第一个比率,而 \(C\) 和 \(D\) 是第二个比率。此公式也可以表示为乘积 \(B \times C\)) 等于乘积 \(A \times D\))。这种关系在理解比例如何起作用方面起着根本性的作用。

比例类型

比例有多种类型：

• 正比例： 当一个数量增加时,另一个数量也会以相同的速率增加。例如,如果工人数量增加一倍,完成的工作也会增加一倍。
• 反比例： 当一个量增加时,另一个量就会减少。例如,如果你增加旅行速度,到达目的地的时间就会减少,因为物理公式是时间 = 距离 / 速度。
• 分割比例： 用于根据给定的比例将整体分成几部分。

正比例与反比例

理解一个非常重要的主题就是正比例和反比例之间的定量差异：

• 正比例： 当 \(x\) 与 \(y\) 成正比时,我们有 \(x = ky\),其中 \(k\) 是一个常数。
• 反比例： 当\(x\)与\(y\)成反比时,我们得到\(xy = k\),其中\(k\)是一个常数。

比例的实际应用

比例不仅仅是一个理论构造,它们可以有许多实际应用,包括：

• 烹饪： 根据份数增加或减少菜谱。
• 金融： 计算利率或投资回报。
• 建造： 确定项目所需的材料数量。
• 药品： 根据患者体重或年龄计算剂量。

如何计算比例？

计算比例：

• 确定比例中的已知值。
• 建立比例方程。
• 使用交叉相乘来求解未知数。
• 通过代入原始方程来验证您的解决方案。

14:7 和 8:4 这两个比例构成比例吗？

我们需要检查一下：

\[ \frac{14}{7} = \frac{8}{4} \]

通过简化,我们简单地得到：

\[ 2 = 2 \]

这意味着两边相等。所以,是的,14:7 和 8:4 这两个比率构成了一个比例,因为它们在简化后相等。

15,2 和 4/30 形成比例吗？

验证方法：

\[ \frac{15}{2} = \frac{4}{30} \]

通过简化：

\[ \frac{15}{2} = 7.5 \] \[ \frac{4}{30} = \frac{2}{15} = 0.1333 \]

因此,答案是否定的,它们不形成比例,因为比率不相等。

比例计算器（带步骤）

以下是我们的比例计算器的操作步骤：

• 输入已知值,通常是 4 个值中的 3 个。
• 计算器将根据提供的输入显示解决比例的逐步过程,其中包括任何所需的交叉相乘和未知变量的求解。
• 它将提供未知值的最终答案以及得出答案所采取的步骤。

带 2 个变量的比例计算器

当处理比例中的两个变量时,情况略有不同,因为您无法立即求解一个变量,而是用另一个变量来表示其中一个未知数：

• 步骤 1：您需要使用已知值和变量建立方程。
• 第 2 步：然后,您将使用代数运算来根据一个变量求解另一个变量。
• 步骤3：最后,您必须输入已知值来找到未知变量。

分数比例计算器

很多时候你可以认为 比例作为分数 。分数比例计算器有助于：

• 将分数转换为小数或百分数,以便于比较。
• 通过简化分数来检查分数是否等价。
• 求解比例中的未知分数。

数学中的比例

您会发现比例在各个数学领域发挥着重要作用,包括以下内容：

• 几何学： 相似三角形和缩放将直接应用边之间的比例
• 代数： 解决涉及比率的方程。这也可能发生在微积分中,当处理相关比率时
• 统计数据： 用于理解数据集中不同的比例关系。通常以样本比例的形式进行分析。

通过理解和应用比例,您可以轻松解决数学和现实场景中的复杂问题。无论您是调整食谱,计算财务回报还是缩放蓝图,比例都是您的数学盟友。

更多比例计算器

如果你正在处理比例,你可能会发现偶然发现相关领域（如样本比例）也很有用。我们的 样本比例计算器 可以帮助您了解比例如何工作以及如何在样本中计算,这在统计分析或处理调查和民意调查时特别有用。

此外,如果您的工作涉及财务分析,业务指标,或者您只是想开始了解财务报表及其解释,我们的 速动比率计算器 可能会引起人们的兴趣。它有助于评估一家公司利用其最具流动性的资产履行短期义务的能力,这间接与理解财务方面的比例有关。

最后,对于那些经常在不同形式的数字之间进行转换的人来说,我们的 分数百分比计算器 和 百分比分数计算器 可以简化这些转换,确保您拥有正确的工具来处理各种格式的比例。