多项式回归计算器

关于这个的更多信息 多项式回归计算器 这样你就能更深入地了解这款计算器提供的结果。

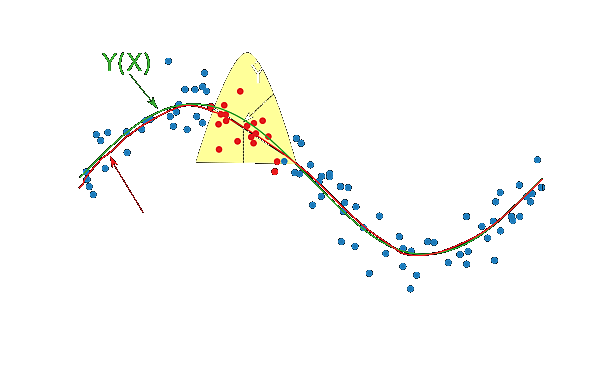
多项式回归与简单线性回归非常相似,只是现在使用一个预测因子及其一定数量的幂来预测因变量 \(Y\)。

什么是多项式回归模型

因此,这里的一个大问题是,如何书写多项式回归方程。多项式线性回归模型的写法是

\[ Y = \displaystyle \beta_0 + \beta_1 X + \beta_2 X^2 + ... + \beta_n X^n + \epsilon\]

其中,\(\epsilon\) 是误差项,它具有正态分布的特性,均值为 0,方差为恒定的 \(\epsilon ~ N(0, \sigma^2)\)。

在提供预测变量 \(X\) 和响应变量 \(Y\) 的样本值后,通过最小化平方误差总和来获得总体斜率系数的估计值。估计模型如下

\[ \hat Y = \displaystyle \hat\beta_0 + \hat\beta_1 X + \hat\beta_2 X^2 + ... + \hat\beta_n X^n\]

如何计算多项式回归？

该程序与大多数回归程序相同：您有一个因变量 \(Y\),希望根据一个或多个预测因子对其进行预测。

在本例中,自变量为 \(X\),预测变量为 \(X\) 及其所有整数幂,直至整数 \(n\),即 \(X, X^2, ...., X^n\)

这是一个带步骤的多项式回归计算器吗？

步骤清晰明了,需要运算的相关矩阵都已标明,矩阵运算也已清楚说明。

要在一个很长的矩阵计算（如本例所需的矩阵计算）中显示过程的每一个代数步骤是不可行的。

如何手工求出多项式回归？

理论上,你可以手工进行计算,但在这种情况下,由于涉及许多变量,计算包括矩阵运算,例如矩阵倒转,手工操作起来非常麻烦。

其他回归计算器

回归是统计学中最常用,用途最广的模型之一,它使用一个或多个预测因子来预测标度因变量 Y 的值。

如果您只想使用一个预测因子,而不想使用功率,可以使用以下方法 简单的线性回归计算器 来代替。或者,如果您有多个预测因子,您需要使用以下方法 多元线性回归计算器 .

回归模型的主要特点之一是假设因变量为区间变量。在很多情况下,我们需要估计一个因变量为二进制（0 - 1）的模型。在这种情况下,我们需要使用 逻辑回归 .