Правила журнала
Логарифмическая функция - одна из самых важных функций в математике, а правила ведения журнала просты и удобны, что значительно упрощает работу с логарифмами.
Давайте сначала вспомним, что означает \(\log_b a\). В этом контексте значение \(b\) является база логарифма, а \(a\) - аргумент .
Мы говорим, что \(\log_b a = y\), когда \(b^y = a\). Это означает, что \(\log_b a\) - это число, до которого необходимо поднять \(b\) (основание), чтобы получить \(a\) (аргумент).
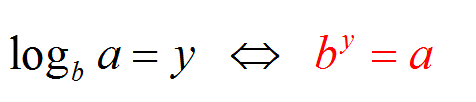
Например, \(\log_{10} 25\) соответствует числу, которое мне нужно поднять до 10, чтобы получить 25. Итак, логарифм, который я ищу, - это число \(y\), которое имеет свойство \(10^y = 25\)
Теперь вопрос в том, как вычислить это число \(y\), которое имеет свойство \(10^y = 25\)? Что ж, это число хорошо определено, и логарифмическая функция \(f(x) = \log_{10} x\) позаботится об этом. Эта функция не является элементарной функцией, и для ее представления необходим ряд Тейлора (бесконечный ряд).
Или вы можете использовать калькулятор (что, наверное, проще, правда?).
Правила журнала: свойства логарифмов
Это основные правила журнала:
Правило # 1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
Правило # 2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
Правило # 3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
Правило # 4 : \(\large \log_a (a) = 1 \)
Правило # 5 : \(\large \log_a (1) = 0 \)
ПРИМЕР 1
Упростите \(\log_2 8 + \log_2 4\) с помощью правил журнала:
ОТВЕЧАТЬ:
Используя Правило №1, мы обнаруживаем, что:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]Итак, первый шаг - это простое применение Правила №1, но как нам получить это \(\log_2 32 = 5\)? Это потому, что \(2^5 = 32\), поэтому в этом случае мы напрямую находим, какое число вам нужно поднять \(2\), чтобы получить \(32\).
Для вычисления большинства логарифмов вам понадобится калькулятор. Это лишь некоторые избранные, которые вы можете вычислить напрямую. Такие вещи, как \(\log_{10} 100 = 2\), потому что вы легко знаете, что \(10^2 = 100\).
Но можете ли вы вычислить \(\log_{10} 102\) напрямую? Нет, для этого нужен калькулятор.
ПРИМЕР 2
Выразите сумму и вычитание логарифмов: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \).
ОТВЕЧАТЬ:
Прежде всего, мы должны помнить, что получение кубического корня - это as, возводя в степень \(1/3\). Другими словами, \(\sqrt[3]{x}\) совпадает с \(x^{1/3}\).
Итак, сначала мы используем Правило № 3, чтобы поставить степень перед логарифмом, а затем мы используем Правила № 1 и № 2. Мы получаем:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]что и требовалось: сумма и вычитание простых логарифмов.
Изменение базовой формулы для логарифмов
Одна из самых полезных формул, относящихся к логарифмам, - это замена основной формулы. Эта формула выглядит так:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]Эта формула просто говорит о том, что если вы хотите изменить базу с \(b\) на \(c\), результаты по сути будут такими же, но вам нужно разделить на логарифм новой базы.
Теперь, если вы художественно ориентированы, вам может понравиться альтернативная форма изменения формулы, описанная ниже:
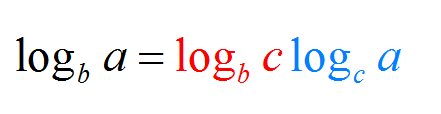
ПРИМЕР 3
Выразите натуральный логарифм \(\ln\) через \(\log\) (основание 10).
ОТВЕЧАТЬ:
Используя замену базовой формулы, получаем:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]Итак, вы говорите, что \(\ln a\) получается делением \(\log a\) на \(\log e\). Насколько удобно? Кто сказал, что математика была трудной, а?
Подробнее о правилах журнала
Логарифмы действительно важны в математике. Исторически логарифмы играют очень важную роль в астрономии как способ предсказания движения Луны и планет.
Логарифмические функции лежат в основе всего в математике, они переплетаются с экспонентами, показателями и почти всем остальным. Вот почему они просят вас выучить логарифмы наизусть, потому что они важны.
Кроме того, эти правила ведения журнала, представленные здесь, играют решающую роль в облегчении разрешение логарифмических уравнений .
Условные обозначения
Есть несколько условных обозначений, о которых вам нужно знать. В общем, мы пишем \(\log_b a\), и мы говорим это "база журнала b of a". Когда база равна \(b = 10\), по соглашению мы просто пишем \(\log a\). Поэтому, когда вы видите \(\log\) без базы, предполагается, что это база \(10\).
Есть еще один примечательный случай. Для \(\log_b a\), когда базой является \(b = e\) (константа Эйлера), мы пишем \(\ln a\) вместо \(\log_e a\). Итак, когда \(\ln\) используется вместо \(\log\), это потому, что основание логарифма - \(e\).
Обратите внимание, что \(\ln a\) обычно называют натуральный журнал . И да, естественные журналы имеют те же правила, что и общие журналы.
Если у вас есть логарифмическая функция, которую вы хотите построить в виде графика, вы можете попробовать наши Создатель графиков логарифмических функций , который предоставит вам аккуратно представленный график.
