Исключение Гаусса - это процесс, проводимый с матрицами, чтобы поместить матрицу в эшелонированная форма . Наличие матрицы в такой форме очень помогает очень легко решать матричные уравнения.

Технически процесс исключения Гаусса заключается в нахождении столбца с точкой поворота (который является модным сленгом для ненулевого элемента), который позволяет нам удалить все элементы ниже точки поворота.

Этот процесс поиска точек поворота и исключения позволяет нам преобразовать матрицу в эшелонированную форму, и процесс идет таким образом, что путем поворота вы добавляете новый столбец в форму эшелона, и вы не "разрушаете" эшелонированную форму. восполнились до предыдущего шага. Красиво, если вы спросите меня.

Термин "эшелонированная форма", полученный с помощью исключения Гаусса, становится понятным, если взглянуть на приведенную выше матрицу, где ненулевые элементы матрицы имеют эту эшелоноподобную структуру, как показано красной линией.

Математика поворота и исключения Гаусса

Мы не будем вдаваться в технические подробности, мы просто постараемся, чтобы вы поняли мотивацию и механику этого вида исключения.

Идея состоит в том, чтобы получить матрицу \(A\) размерности \(m \times n\) (то есть, она имеет \(m\) строк и \(n\) столбцов) в другой форме, более удобной для решения уравнений.

В частности, для матрицы \(m\times n\) \(A\) и вектора \(m\times 1\) \(b\) нам нужно найти вектор \(n\times 1\) \(x\) такой, что

Вы можете подумать: "Это так просто, мы просто умножаем каждую сторону на \(A^{-1}\) слева" и получаем:

....Не так быстро! Это работает только тогда, когда матрица \(A\) обратима. Для начала матрица \(A\) должна быть квадратной матрицей, а затем ее определитель должен отличаться от нуля. Но вы не можете умножить на обратное для неквадратных матриц. Итак, как же тогда это сделать?

Вам нужно ПРЕОБРАЗОВАТЬ уравнение в более простое для решения.

В частности, матрицы в эшелонированной форме представляют собой матрицы, которые приводят к уравнениям, которые легко решить (подробнее об этом позже).

Использование элементарных матриц

Прежде всего, сделаем одно важное замечание. Если у нас есть решение матричного уравнения \(Ax = b\), а \(E\) - обратимая матрица, то \(x\) также является решением \((EA)x = Eb\), и наоборот.

Другими словами, матричные уравнения

а также

эквивалентны для обратимой матрицы \(E\). Что мы подразумеваем под тем, что уравнения эквивалентны? Мы имеем в виду, что уравнения имеют одинаковые решения.

Итак, что мы собираемся сделать, это начать с \(Ax = b\), и, умножая на обратимые матрицы \(E\), мы собираемся прийти к эквивалентному матричному уравнению, которое намного проще решить .

Скажем, мы можем найти список обратимых матриц \(E_1, E_2, ..., E_n\), и мы умножаем (слева) исходное матричное уравнение, чтобы преобразовать его в эквивалентное уравнение, например:

где \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) и \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\).

Наша цель - тщательно выбирать обратимые матрицы \(E_1, E_2, ..., E_n\), так что \(\tilde A\) находится в эшелонированной форме.

Это почему? Потому что, если \(\tilde A\) находится в эшелонированной форме, решение матричного уравнения \(\tilde A x = \tilde b\) намного проще, и мы уже знаем, что \(\tilde A x = \tilde b\) имеет те же решения, что и \(A x = b\)

ПРИМЕР 1

Давайте разберемся, почему решение матричного уравнения намного проще, если оно имеет эшелонированную форму. Сначала представьте, что у вас есть следующие матрица и вектор:

и вы хотите решить \(Ax = b\). Как бы выглядела система уравнений? Система \(Ax = b\) будет выглядеть так

Как это выглядит? Ну, не так уж и красиво. Вам нужно будет начать жонглировать уравнениями. Существуют более или менее систематические подходы к решению этой проблемы с использованием таких вещей, как устранение и тому подобное, но это, по крайней мере, громоздко.

Теперь, с другой стороны, представьте, что у вас есть следующие матрица и вектор:

и вы хотите решить \(\tilde A x = \tilde b\). В этом случае матрица \(\tilde A\) имеет эшелонированную форму. Как бы выглядела система уравнений? Система \(\tilde A x = \tilde b\) будет выглядеть так

Как это выглядит? Что ж, не так уж и плохо.

В самом деле, если мы начнем непосредственно с третьего уравнения, мы получим \(x_3 = -1\) напрямую. Затем из второго уравнения \(x_2 = -1 + x_3 = -1 + (-1) = -2\). И из первого уравнения \(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\). Итак, без всяких сомнений, мы обнаружили, что:

Следовательно, в этом случае система решается тривиально.

Для систем, связанных с матрицами в эшелонированной форме, легко вернуться от последнего уравнения к первому уравнению, чтобы получить решения.

Как правильно выбрать обратимые матрицы

Теперь, когда мы знаем, что работа с матрицами в эшелонированной форме значительно упрощает решение матричных уравнений, нам должно быть интересно, какие же обратимые матрицы \(E_1, E_2, ..., E_n\) сделают \(\tilde A\) эшелонированной формой.

Как работает метод исключения Гаусса?

Интересно, что найти эти матрицы \(E_1, E_2, ..., E_n\), которые мы будем называть элементарными матрицами, несложно.

Шаг 1 : Посмотрите на первый столбец, если он имеет ненулевое значение, это будет ваша точка опоры. Если первая строка первого столбца не равна нулю, используйте ее как сводную. Если нет, найдите строку с ненулевым значением и переставьте эту строку и первую строку.

Итак, вы нашли стержень, и, возможно, вам нужно сделать перестановку строк (которая фактически представлена умножением на некоторую обратимую матрицу)

Шаг 2 : Как только у вас есть точка поворота, удалите все элементы в текущем столбце под точкой поворота.

Это делается путем умножения строки сводной таблицы на определенную константу и добавления ее к строке под сводной точкой, так что элемент в том же столбце, что и сводная точка, становится нулевым.

Шаг 3 : После того, как все элементы ниже точки поворота были обнулены путем выполнения соответствующих операций со строками (которые, как оказалось, представлены операцией обратимой матрицы), переходите к следующему столбцу, следующей строке и ищите точку поворота в строке ниже ряда предыдущего стержня и проделайте ту же процедуру.

Шаг 4 : Повторяйте до тех пор, пока у вас не закончатся столбцы или пока матрица не перейдет в эшелонированную форму.

ПРИМЕР 2

Используя вращение и исключение Гаусса, решите следующую систему:

ОТВЕЧАТЬ:

Прежде всего, соответствующие матрица \(A\) и вектор \(b\):

Расширенная матрица \([A|b]\) есть

Чтобы решить эту систему, нам нужно пройти гауссовское исключение. Выбираем первую опору, начиная с первого столбца. Элемент в первой строке первого столбца равен 1, который отличается от нуля, и затем он используется в качестве точки поворота. Мы используем этот стержень (1), чтобы удалить все элементы под ним:

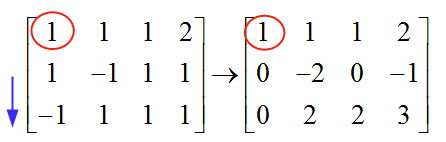
Механизм устранения элементов ниже оси прост. В этом случае, чтобы исключить "1", которая находится ниже точки поворота, я вычитаю элементы в строке 1 из элементов в строке 2. Таким образом я формирую ноль под точкой поворота.

Точно так же, чтобы исключить "-1" в строке 3, я добавляю элементы в строке 1 к элементам в строке 3. Таким образом я формирую ноль под точкой поворота в строке 3.

Мы увидим, что эти операции со строками достигаются путем умножения на обратимую матрицу, поэтому у нас есть эквивалентные системы, делая это.

Теперь, переходя к следующей строке, следующему столбцу, мы находим "-2", который отличается от нуля, и, следовательно, он используется в качестве нашей точки поворота. Чтобы исключить значение ниже этой точки поворота, мы добавляем в строку 3 значения строки 2:

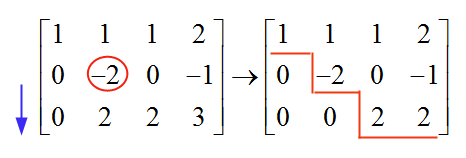
и теперь мы останавливаемся, потому что получившаяся матрица уже находится в эшелонированном виде. Теперь мы возвращаемся, чтобы решить систему: