Правило Крамера
Правило Крамера - это метод, используемый для систематического решения систем линейных уравнений, основанный на вычислениях определителей.
Обычно решение системы линейных уравнений может быть беспорядочным для систем размером более 2x2, потому что есть много способов уменьшить его, когда есть три или более переменных.
Правило Крамера обеспечивает однозначный и систематический способ поиска решений систем линейных уравнений независимо от размера системы.
Количество требуемых вычислений увеличивается для больших систем, но процедура остается неизменной, независимо от размера системы.
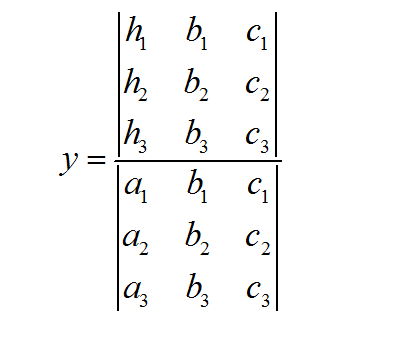
Как использовать правило Крамера
Чтобы упростить задачу, мы рассмотрим случай \(n = 2\), а затем создадим более общую версию, которая, будем надеяться, станет лучше после рассмотрения случая \(n=2\).
Шаг 1
: Все линейные системы 2x2 можно записать в следующем виде:
Итак, ваш первый шаг - найти эти значения \(a_1, b_1, c_1\) и \(a_2, b_2, c_2\) для системы, которую вы хотите решить.
Шаг 2
: Получив коэффициенты \(a_1, b_1, c_1\) и \(a_2, b_2, c_2\), вы используете следующие формулы для решения \(x\) и \(y\):
В приведенной выше формуле "det" означает определитель соответствующей матрицы. Иногда для определителей используются более компактные обозначения, как показано ниже:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]Итак, используя обозначения выше, мы получили бы эти более компактные формулы для правила Крамера:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]Позвольте нам визуально понять, что происходит. Обратите внимание, что и \(x\), и \(y\) имеют один и тот же определитель в знаменателе.
Коэффициенты этой общей матрицы, используемые в знаменателе, напрямую выводятся из коэффициентов, которые умножают \(x\) и \(y\) в системе. См. Изображение ниже:
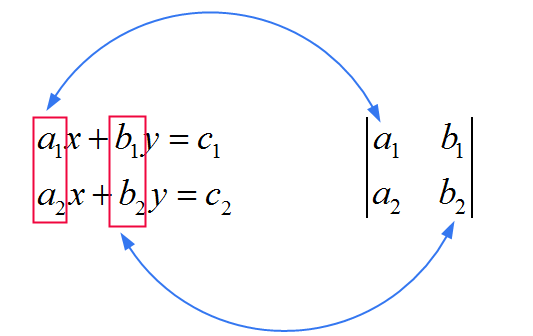
Теперь мы видим, что \(x\) и \(y\) отличаются тем, что указано в числителе. Подумайте об этом, чтобы запомнить правило:
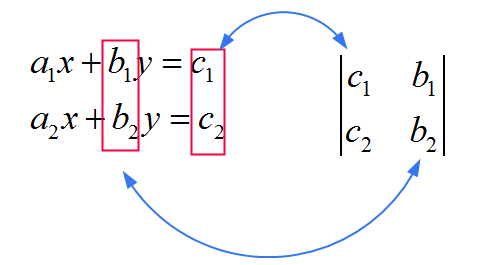
Для \(x\) вы используете ту же матрицу, что и матрицу в знаменателе, только вы заменяете ПЕРВЫЙ столбец на коэффициенты \(c_1\) и \(c_2\). См. Изображение ниже
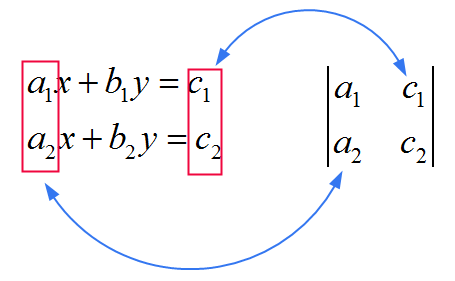
Для \(y\) вы используете ту же матрицу, что и в знаменателе, только вы заменяете ВТОРОЙ столбец на коэффициенты \(c_1\) и \(c_2\). См. Изображение ниже
ПРИМЕР 1
Решите следующую линейную систему 2x2:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]ОТВЕЧАТЬ:
Давайте выполним два описанных выше шага, чтобы использовать правило Крамера для решения системы, описанной выше:
Шаг 1
: Нам нужно определить коэффициенты для соответствующих определителей.
Для матрицы, входящей в знаменатель, мы используем
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]Теперь, в этом случае \(c_1 = 10, c_2 = 4\), для определителя, используемого для вычисления \(x\), мы заменяем предыдущую матрицу, изменяя ПЕРВЫЙ столбец:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]Для определителя, используемого для вычисления \(y\), мы заменяем предыдущую матрицу, изменяя ВТОРОЙ столбец:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]Итак, теперь мы получили решение:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]и для \(y\):
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]Следовательно, решение \(x = 3\), \(y = 1/2\).
Правило Крамера для общего случая
Прелесть правила Крамера в том, что оно применяет точно такую же процедуру, независимо от того, является ли это системой 2x2 или системой 10x10. Концепция та же.
Итак, предположим, что \(x_1, x_2, ..., x_n\) - переменные (неизвестные), и мы хотим решить следующую систему линейных уравнений размера nxn:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]Чтобы найти \(x_1, x_2, ..., x_n\), мы будем использовать следующий определитель в знаменателе:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• Решением для \(x_1\) является
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• Решением для \(x_2\) является
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]И так далее. Как видите, определитель в знаменателе тот же, а в числителе получен путем изменения первого столбца с \((c_1, ..., c_n)\) на \(x_1\). Для \(x_2\) мы меняем второй столбец на \((c_1, ..., c_n)\), для \(x_3\) мы меняем третий столбец и так далее. Вы уловили идею.
ПРИМЕР 2
Решите следующую систему линейных уравнений 3x3, используя правило Крамера.
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]ОТВЕЧАТЬ:
Прежде всего, мы идентифицируем определитель, который стоит в знаменателе:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]Также нам нужно определить вектор коэффициентов \(c_i\):
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]Этот вектор будет тем, который заменит соответствующие столбцы общего определителя из знаменателя. Мы получаем:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]Подробнее о правиле Крамера
Правило Крамера играет особую роль в эффективном решении систем линейных уравнений. Он включает использование детерминантов, чтобы упростить задачу, которая в противном случае была бы действительно сложной, особенно для более крупных систем.
В конечном итоге, чтобы решать линейные системы , все, что вам нужно сделать, это определить определители числовой матрицы на основе системы, которую необходимо решить, и провести простую алгебраическую операцию для решения этой системы.
Приложения
Правило Крамера имеет множество приложений как в линейной алгебре, так и в дифференциальных уравнениях.