Метод замены интеграции
Метод замещения интеграции или интеграции методом замещения является умным и интуитивным методом, используемым для решения интегралов, и он играет решающую роль в обязанности решения интегралов наряду с Интеграция по частям а также Разложения частичных фракций метод.
Интеграция может быть сложной операцией по времени, и у нас есть только несколько инструментов, доступных для продолжения.
Естественно, расчет неопределенного интеграла для некоторых основных элементарных функций (таких как полиномы, мощности, элементарные тригонометрические функции и т. Д.) очень просто.
Но вопрос в том, как действовать с вычислением неопределенного интеграла (или примитивного) для более сложных функций или для алгебраической комбинации функций.
Вы готовы рок ??Я так следи за мной.
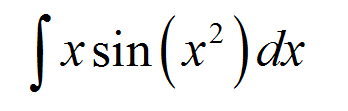
Как работает метод замещения?
Способ интеграции путем замещения работает путем определения "блока", который содержит переменную интеграции, так что производное этого блока также можно найти внутри интеграла.Этот метод также обычно называется методом U-подстановки.
Если структура интеграла позволяет, этот "блок" становится фактически новой интеграционной переменной, если все идет хорошо, и интеграл становится серьезно упрощенным.
Это всегда работает?Нет. Или по-другому, вы всегда можете сделать замену, но он не всегда преобразует его в более легкий интеграл.
Почему даже попробовать этот метод?Ну, потому что это работает часто.И, как правило, первый трюк, который вы должны попробовать, если вам нужно решить интеграл, который не тривиален.
Давайте выпустим пару шагов, чтобы следовать, если вам нужно применить этот метод:
ШАГ 1:
Осмотрите функцию, которую вы интегрируете и ищите "блок", это функция \(x\), которая появляется одно или несколько раз в функции, которую вы интегрируете.
ШАГ 2:
"Блок", который вы ищете должны иметь очень конкретное свойство: производное блока необходимо появиться один раз и один раз только в функции, которая интегрирована.
ШАГ 3:
Если предыдущие шаги были успешными, вы можете использовать "блок" в качестве новой переменной, и вы можете заменить переменную и дифференциал на новую переменную, а интеграл, который вы решаете, теперь становится намного проще.
Техническая нота Обычно я пытаюсь сохранить все объяснения простыми и стараться избегать технических данных.В этом случае мне придется дать техническое объяснение метода замещения, чтобы не оставлять вещи слишком неформально с идеей "блока".
Если вам не нравятся технические данные, вы можете пропустить следующий раздел, где вы увидите примеры.
Итак, вся идея состоит в том, чтобы интегрировать данную функцию \(f(x)\).Поэтому нам нужно найти:
\[\int f(x) \, dx\]Скажите, что функция \(f(x)\) - это не просто функция, и она имеет определенную конкретную структуру, специально
\[f(x) = g(h(x))h'(x)\]И предположим, что есть функция \(G(x)\), так что \(G'(x) = g(x)\) (так что \(G\) - это антиверанс \(g\)).Тогда мы получаем это
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]Это почему??? Ну, просто: по определению, антидидирующий - это функция, так что, когда вы ее дифференцируете, вы получаете функцию, которую вы интегрируете.
В этом случае, если вы дифференцируете \( G(h(x)) \), вы получаете
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]По правилу цепи ..... и Шазам!у тебя есть это.Сказал тебе, что это не так сложно.
Примеры методов замещения
Лучший способ узнать о том, как интегрировать - это практиковать.Некоторые люди будут радоваться взглядом на доказательства, но большинство людей захотят видеть вещи на практике.
Итак, давайте перейдем к практическим основаниям.
Пример 1.
Найдите следующий неопределенный интеграл:
\[\int x \sin(x^2)\,dx\]ОТВЕЧАТЬ:
Согласно шагу 1, мы ищем блок, очень конкретный блок.Если вы посмотрите на интеграл, переменная интеграции \(x\).
Есть много испытаний и ошибок, потенциально, при использовании этой техники.Сказать, что мы рассмотрим следующий блок:
\[u = x^2\]Мы знаем, что этот блок хорош, потому что производное из него является \(u' = 2x\), который появляется в интеграл.
Но тогда вы говорите: "Я вижу \(x\), но я не вижу 2".Ну, нет необходимости беспокоить.Мы можем сделать трюк.Соблюдайте это
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]Кто ты, Mandrake Magiciкусник ???Помимо шутит, этот маленький трюк работает.Итак, замена блока
\[u = x^2\] \[du = 2x \, dx\](Обозначение \(du = 2x \, dx\) является разрешительным и технически неверным, но у него есть прочная основа, поэтому медведь с ним).Так что делая эту замену преобразовать интеграл на
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]Итак, как только вы изменились на новую переменную __xxyz_a__, интеграл вступил в более легкую решить интеграл \(\sin(u)\).Как только вы решите его, вы должны помнить, чтобы вернуться к исходной переменной.
Пример 2.
Теперь давайте перейдем к немного более сложному примеру.Вычислить неопределенный интеграл
\[\int e^{x+e^x} \,dx\]используя метод U-подстановки.
ОТВЕЧАТЬ:
Что ты говоришь ???Ну, это не так сложно.Обратите внимание, что неопределенный интеграл может быть повторно написан как:
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]Итак, теперь, когда вы видите новую форму функции, которую вы интегрируете, можете ли вы придумать "блок" или "U-подстановку" ??
Помните, не стесняйтесь делать проб и ошибку.Если что-то не работает, попробуйте что-нибудь еще.Что если вы попробовали \(u = e^x\)?
Производное блока \(u' = e^x\), которое найден один раз в оригинальной функции.Кроме того:
\[u = e^x\] \[du = e^x \, dx\]Итак, мы получаем:
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]Подробнее о интеграции путем замены
Давайте столкнемся к этому: интеграция может быть тяжелой.Очень трудно.Некоторые не слишком сложные функции (по крайней мере по внешности) дали математики ужасно трудно разобраться с.
Некоторые другие не слишком сложные функции (по крайней мере по внешности) просто не разрешаются элементарными методами.
Итак, вам лучше полагать, что интеграция может быть жестким испытанием.Так что вы должны пойти подготовиться.
Один из самых простых инструментов, и очень часто используемая техника - это методика интеграции путем замены.Да, он используется, потому что он часто появляется на тестах или домашнем задании.
Но мы немного изменяли.На самом деле, интегралы, которые имеют правильную структуру, которая будет решена методом замещения, очень специфична.Причина, по которой вы видите много примеров этого, заключается в том, что они являются очень специфическими функциями, которые предназначены для работы, чтобы быть интегрированы с этой методикой.
Но позвольте мне быть тусклым: если у вас есть программная программа, которая предназначена для создания случайных функций, и она генерирует для вас, шансов, что вы сможете использовать методику замещения Slim.
Тем не менее, это мощная маленькая технология интеграции, которая работает для очень конкретного класса интегралов.
Что такое методика U-подстановки?
𝘶-замещение неопределенных интегралов - это просто другое имя для метода замещения.Он называется "𝘶-замещение", потому что блок, который используется назван \(u\), поэтому новая переменная будет u.
Это определенно не хорошее имя, потому что имя, которое вы выбираете для вашего блока, совершенно не относятся к процессу вычисления интеграла.Вы можете назвать блок (и новую переменную) \(z\), и это не имеет значения.