Эластичность дуги для таблицы спроса
Инструкции: Используйте этот калькулятор для вычисления формулы дуговой эластичности для таблицы значений с ценой (P) и требуемым количеством (Q). Введите или вставьте ваши данные в электронную таблицу ниже.
Формула упругости дуги для таблицы
Формула дуговой эластичности спроса позволяет оценить эластичность в точках, указанных в таблице графика спроса, не имея явной формулы для функции спроса.
Вам нужно предоставить таблицу со столбцом для цены и столбцом для требуемого количества. После того, как вы введете или вставите это в предоставленную электронную таблицу, вы нажмете "Рассчитать", чтобы получить соответствующие дуговые эластичности, рассчитанные для вас.
Обратите внимание, что это всего лишь приближение: идеальная ситуация — вычислить эластичность, используя функцию спроса , используя производные.
Шаги по использованию arc-elasticity для таблицы
\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]и это может быть применено к последовательным точкам в таблице графика спроса. Вы будете следовать этим шагам:
- Шаг 1: Правильно занесите в таблицу значения цены (P) и объема спроса (Q)
- Шаг 2: Вы можете создать столбцы для Q2 - Q1, P2 - P1, Q1 + Q2 и P1 + P2, если хотите сделать вычисления более понятными, или вы можете вычислить формулу напрямую
- Шаг 3: В таблице будет пропущена одна точка, так как дугообразная упругость берет точку в таблице и точку, которая непосредственно следует за ней в таблице
Использование этого приближения дуговой эластичности даст вам прекрасную картину чувствительности к изменению цен на конкретный анализируемый товар, даже если это всего лишь приближение.
Чем больше точек спроса, тем точнее будет аппроксимация, особенно если эти ценовые точки близки друг к другу.
Что измеряет эластичность дуги?
Дуговая эластичность направлена на обеспечение приближения истинной эластичности в заданной точке. Фактическая эластичность из кривой спроса вычисляется по формуле:
\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]Можно утверждать, что дуговая эластичность — это всего лишь приближение, так как же тогда она имеет какую-то ценность? Ответ на это заключается в том, что для анализа эластичности и анализа чувствительности в экономике в целом нас больше интересуют диапазоны, чем очень конкретные точки.
Действительно, для целей микроэкономики полезно знать, находимся ли мы в неэластичном диапазоне или нет, а не конкретное значение эластичности
Это не значит, что конкретное значение неважно, поскольку его наличие действительно полезно, но дуговые эластичности часто являются хорошим приближением и дают нам очень точное представление о том, с каким типом диапазона эластичности мы сталкиваемся.
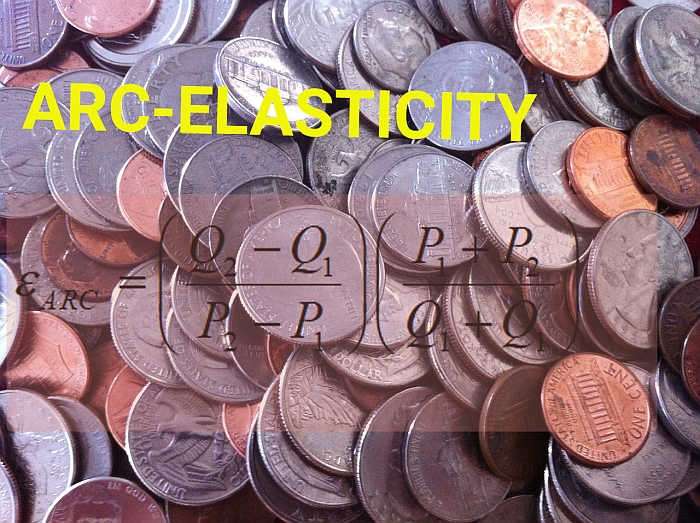
Пример
Рассмотрим следующую таблицу спроса с информацией о цене и требуемом количестве
Укажите приближение упругости дуги для точек данных в этой таблице.
| П | В |
| 1 | 200 |
| 1.5 | 190 |
| 2 | 170 |
| 2.5 | 155 |
| 3 | 130 |
| 3.5 | 110 |
| 4 | 90 |
| 4.5 | 60 |
Решение: Чтобы приблизительно рассчитать эластичность спроса по цене на основе этих данных, нам необходимо использовать следующую формулу дуговой эластичности:
\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]Применяя приведенную выше формулу ко всем парам последовательных точек данных, мы находим следующие дуговые эластичности:
| П | В | Эластичность Дуги |
| 1 | 200 | - |
| 1.5 | 190 | \(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\) |
| 2 | 170 | \(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\) |
| 2.5 | 155 | \(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\) |
| 3 | 130 | \(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\) |
| 3.5 | 110 | \(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\) |
| 4 | 90 | \(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\) |
| 4.5 | 60 | \(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\) |
Интерпретация
Найденная таблица показывает приблизительную ценовую эластичность спроса для каждой из предоставленных ценовых точек. Эти значения можно приблизительно использовать для определения эластичных и неэластичных диапазонов для предоставленного графика спроса.
Другие экономические калькуляторы
Если вы работаете в области эконометрики, это Калькулятор регрессии вероятно, будет полезным, особенно потому, что он показывает все этапы процесса расчет коэффициентов регрессии .
Вы также можете использовать логарифмическое уравнение оценить кривая спроса с постоянной эластичностью .
