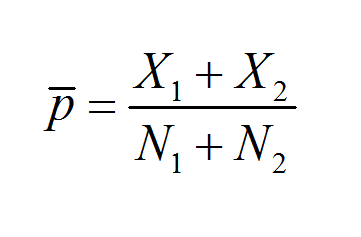Proportions Calculator

This calculator will help you with the calculation of a proportionality relation A / B = C / D, for which you need to provide three of the four numerical expression to find the missing one. Also, you could provide all four of them and the calculator in that case will assess whether or not the proportionality holds for the numbers provided.

Once you provide the requested numerical expressions (which could be numbers or any valid numeric expression), you can then click on the "Calculate" button to be presented with the result of the calculations.

How to Use this Proportions Calculator?

Using this proportions calculator will simplify solving mathematical proportions for you. Here are the steps you should follow:

• Identify the proportionality: Establish the proportion that you need to compute
• Input the Known Values: Enter the known values into the provided boxes, you need three numbers out of the four numbers involved in the proportion.
• Calculate: Click on the calculate button to get the result. The calculator will show you the missing value.

Steps to Solve Proportions

Here is how you can manually solve proportions:

• Set Up the Proportion: Write the ratios in fraction form, like \(\frac{A}{B} = \frac{C}{D}\).
• Cross Multiply: Multiply the numerator of the first fraction by the denominator of the second, and vice versa: \(A \times D = B \times C\).
• Solve for the Unknown: If you're solving for \(x\), rearrange the equation to isolate \(x\).
• Check Your Work: Ensure the ratios are equal by substituting the found value back into the original proportion.

Proportion Formula Explained

The basic formula for a proportion is:

\[ \frac{A}{B} = \frac{C}{D} \]

Where \(A\) and \(B\) are the first ratio, and \(C\) and \(D\) are the second ratio. This formula can also be expressed as having the product \(B \times C\)) equal to the product of \(A \times D\)). This relationship is plays a fundamental role in the understanding of how proportions work.

Types of Proportions

There are several types of proportions:

• Direct Proportion: When one quantity increases, the other increases at the same rate. For example, if you double the number of workers, the work done also doubles.
• Inverse Proportion: As one quantity increases, the other decreases. For instance, if you increase the speed of travel, the time to reach a destination decreases, because of the physics formula time = distance / speed.
• Partitive Proportion: Used when dividing a whole into parts according to given ratios.

Direct Proportion vs. Inverse Proportion

One topic that is very important to understand is that of the quantitative difference between direct and inverse proportions:

• Direct Proportion: When \(x\) is directly proportional to \(y\), we have \(x = ky\) where \(k\) is a constant.
• Inverse Proportion: When \(x\) is inversely proportional to \(y\), we have \(xy = k\), where \(k\) is a constant.

Real-Life Applications of Proportions

Proportions are not just a theoretical construct, and they can have numerous practical applications including:

• Cooking: Scaling recipes up or down based on the number of servings.
• Finance: Calculating interest rates or investment returns.
• Construction: Determining the amount of materials needed for a project.
• Medicine: Dosage calculations based on patient weight or age.

How Do I Calculate a Proportion?

To calculate a proportion:

• Identify the known values in the proportion.
• Set up the proportion equation.
• Use cross multiplication to solve for the unknown.
• Verify your solution by substituting back into the original equation.

Do the Ratios 14:7 and 8:4 Form a Proportion?

We need to check it:

\[ \frac{14}{7} = \frac{8}{4} \]

By simplifying, we simply get:

\[ 2 = 2 \]

which implies that both sides are equal. So, yes, the ratios 14:7 and 8:4 form a proportion because they are equal when simplified.

Does 15, 2, and 4/30 Form a Proportion?

To verify:

\[ \frac{15}{2} = \frac{4}{30} \]

By simplifying:

\[ \frac{15}{2} = 7.5 \] \[ \frac{4}{30} = \frac{2}{15} = 0.1333 \]

Therefore, the answer is NO, these do not form a proportion as the ratios are not equal.

Proportions Calculator with Steps

Here's how our proportions calculator with steps works:

• Input the known values, which is usually 3 out of the 4 values.
• The calculator will show the step-by-step process of solving the proportion based on the inputs provided, which includes any required cross-multiplication and the solving for the unknown variable.
• It will provide the final answer for the unknown value along with the steps taken to reach the answer.

Proportion Calculator with 2 Variables

When dealing with two variables in a proportion the situation is slightly different because you cannot immediately solve for one variable, but you rather will express one of the unknowns in terms of the other:

• Step 1: You need to set up the equation with the known values and the variables.
• Step 2: Then, you will use algebraic manipulation to solve for one variable in terms of the other.
• Step 3: Final you have to input the known value to find the unknown variable.

Fraction Proportion Calculator

Often times you can regard proportions as fractions. A fraction proportion calculator helps in:

• Converting fractions to decimals or percentages for easier comparison.
• Checking if fractions are equivalent by simplifying them.
• Solving for unknown fractions in a proportion.

Proportions in Mathematics

You will find that proportions play a significant role in various mathematical fields, including the following:

• Geometry: Similar triangles and scaling will directly apply proportions between sides
• Algebra: Solving equations involving ratios. This could also occur in Calculus, when dealing with related rates
• Statistics: Used to understand different proportional relationships in data sets. Usually analyzed in the form of sample proportions.

By understanding and applying proportions, you can solve complex problems in mathematics and real-world scenarios with ease. Whether you're adjusting a recipe, calculating financial returns, or scaling a blueprint, proportions are your mathematical ally.

More Proportion Calculators

If you're working with proportions, you might find it useful to also stumble upon related areas, like sample proportions. Our Sample Proportion Calculator can help you understand how proportions work and are calculated within a sample, which is particularly useful in statistical analysis or when dealing with surveys and polls.

Additionally, if your work involves financial analysis, business metrics, or you simple want to get started with financial statements and their interpretation, our Quick Ratio Calculator could be of interest. It helps in assessing a company's ability to meet its short-term obligations with its most liquid assets, which indirectly relates to understanding proportions in financial terms.

Lastly, for those who often convert between different forms of numbers, our Fraction to Percentage Calculator and Percent to Fraction Calculator can simplify these conversions, ensuring you have the right tools to work with proportions in various formats.