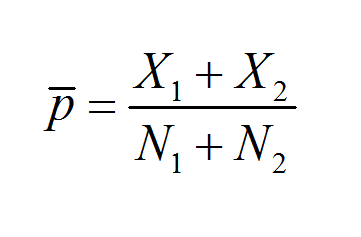About this Sample Proportion Calculator

With this sample proportion calculator you will be able to provide favorable cases and total cases to get the actual sample proportion. This process is widely used, especially when doing polling analyses.

Once you provide a number of favorable cases and total sample size, you need to click on "Calculate" to get the results and interpretation of the calculations.

Sample proportions are a crucial concept in Statistics, due to the fact that a sample proportion can be regarded as a actual average of n Bernoulli(p) variables, for which reason the Central Limit Theorem applies when the sample size is sufficiently large (\(n \ge 30\)).

This, in practical terms indicates that we can use the normal distribution to compute proportion probabilities.

What does the sample proportion represent?

The sample proportion, defined as favorable cases divided by total number of cases, represent that proportion that group is with respect to the total number of cases. In terms of a formula, we have the following:

\[ \hat p = \displaystyle \frac{ \text{Favorable Case} }{ \text{ Total Cases} } = \displaystyle \frac{X}{N} \]

For example, a sample proportion of 0.55 indicates that number of favorable cases are 55% of total number of cases, which gives us a very good indication of the size of one specific group with respect to the total.

What are the steps for finding the sample proportion?

• Step 1: Identify the number of favorable cases (X) and the total number of cases (N)
• Step 2: You can proceed only if both the favorable cases and total number of cases are integer, and the number of favorable cases does not exceed the number of total cases
• Step 3: You use the formula \(\hat p = \displaystyle \frac{X}{N}\)
• Step 4: You can multiply the sample proportion \(\hat p\) by 100 to get the associated percentage

Proportion sampling is crucial when doing polling analysis doing an election process, where suitable sampling could lead to an early prediction of the winner. The sample proportion is a pointwise estimator only though, and in order to conduct inferential claims, it is necessary to find a confidence interval for the sample proportion.

What is the sample proportion symbol?

The sample proportion symbol is traditionally \(\hat p\), which obviously comes from the fact that it is a estimator of the true population proportion \(p\). Some textbooks will use notation like \(\hat{\pi}\), but it is relatively uncommon.

The idea of having to use a special symbol appears a redundant, but yet, if we had to write the long form "sample proportion" every time we need to refer to it, it becomes truly cumbersome, and the existence of a clear, unequivocal symbol comes in handy.

Why dealing with sample proportions

Since often times we don't know what is the actual population proportion, working with sample data instead looks like a good option, especially if the sampling process was random and ideally representative of the whole population.

By virtue of Chebyshev's Theorem, the sample proportion will converge to the true population proportion, and there we have an excellent proxy of the true population information.

Example

In a voting process of a social club, it was found that a total of N = 120 members voted, and X = 65 voted for Candidate A. What percentage of voters in the club favor candidate A?

Solution: The sample proportion is

\[ \hat p = \displaystyle \frac{ \text{Favorable Case} }{ \text{ Total Cases} } = \displaystyle \frac{65}{120} = 0.5417 \]

This implies that 54.17% of voters in the club favor Candidate A. This concludes the calculation.

More Statistic Calculators

Using sampling distributions for the proportion have the consequence that normal probabilities can be used, which is a great advantage, and even more so when it can be used at the level of normal sampling distributions, where the variability gets reduced by a factor of \(\sqrt n\).

Sampling proportions are also the main ingredient of confidence intervals for proportions and z-test for proportions.