लॉग ग्राफ़ खोजने का तरीका सभी लॉगरिदमिक फ़ंक्शन के लिए सामान्य है। इसका कारण यह है कि सभी लघुगणकीय कार्यों में अनिवार्य रूप से एक ही आकार होता है, कम से कम संरचनात्मक रूप से, यह केवल लघुगणक के आधार पर निर्भर करता है।

सबसे पहले, आइए हम आधार \(a\), \(\log_a x\) के साथ लघुगणकीय फलन को याद करें। उपयोग किए जाने वाले सबसे विशिष्ट आधार \(a = 10\) के लिए हैं, जिस स्थिति में हम केवल \(\log x\) लिखते हैं, और जिस स्थिति में \(a = e\), उस स्थिति में हम \(\ln x\) लिखते हैं, और हम इसे प्राकृतिक लॉग कहते हैं।

उदाहरण के लिए, प्राकृतिक लॉग फ़ंक्शन का ग्राफ, \(\ln x\) नीचे दिखाया गया है:

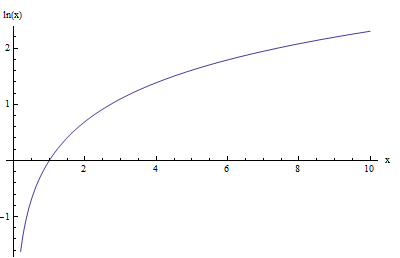
अब, देखते हैं कि क्या होता है जब हम \(\log x\) और \(\ln x\) को एक साथ ग्राफ़ करते हैं (यह लॉग बेस 10 और प्राकृतिक लॉग है):

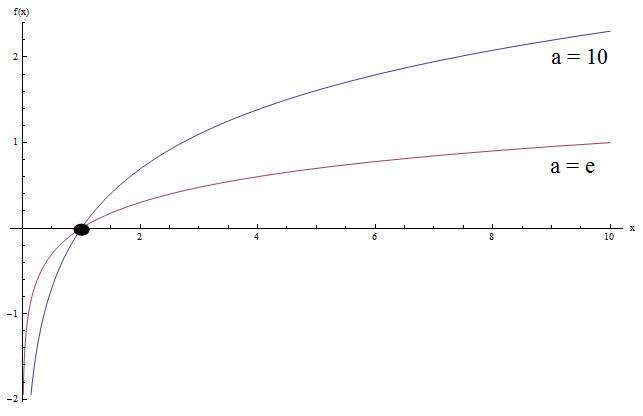
क्या आप कोई समानता देखते हैं? खैर, कुछ हैं।

ध्यान दें कि दोनों ग्राफ़ का सामान्य अवतल आकार समान है। साथ ही, दोनों ग्राफ \(x = 1\) पर y-अक्ष को पार करते हैं (जो \(a > 0\) के साथ सभी आधारों के लिए \(\log_a 1 = 0\) के बाद से कोई आश्चर्य की बात नहीं है)।

एक और बात यह है कि दोनों ग्राफ नकारात्मक अनंत तक पहुंचते हैं जब \(x\) 0 तक पहुंचते हैं, और अनंत तक \(x\) अनंत तक पहुंचते हैं।

क्या होगा यदि हम \(0 < a < 1\)? के साथ लघुगणकीय कार्यों को रेखांकन करने का प्रयास करते हैं? नीचे दिए गए उदाहरण की जाँच करें:

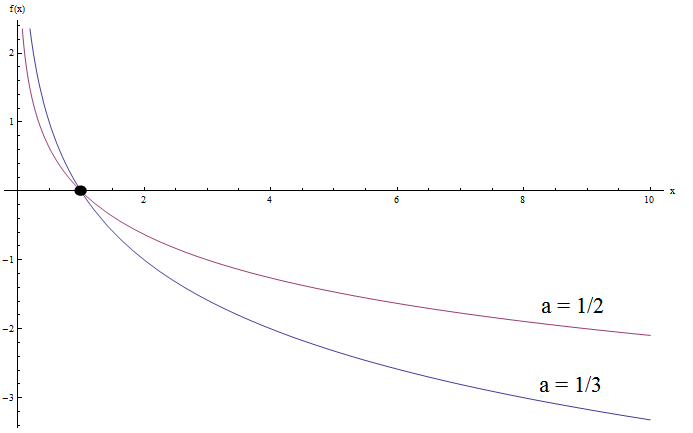
क्या अब आप कोई समानता देखते हैं? बेशक।

ध्यान दें कि दोनों ग्राफ़ का सामान्य उत्तल आकार समान है। साथ ही, दोनों ग्राफ फिर से y-अक्ष को \(x = 1\) पर पार करते हैं, जो अपेक्षित है।

लेकिन अब दोनों ग्राफ़ अनंत तक पहुँचते हैं जब \(x\) 0 पर पहुँचता है, और ऋणात्मक अनंत तक \(x\) अनंत तक पहुँचता है। यह एक तरह का विपरीत व्यवहार है जब आधार \(a\) 1 से बड़ा होता है।

आप लॉग ग्राफ कैसे बनाते हैं?

पिछले उदाहरणों में हमने जो पाया, उसके आधार पर, हम कुछ नियमों में डाल सकते हैं जिनका उपयोग आप तब कर सकते हैं जब आप लॉग ग्राफ़ बनाना चाहते हैं:

मान लें कि आप \(a > 0\) के लिए फंक्शन \(y = \log_a x\) को ग्राफ़ करना चाहते हैं। फिर:

चरण 1 : हमेशा, लॉगरिदमिक फ़ंक्शन y-अक्ष को \(x = 1\) पर पार करता है।

चरण 2 : यदि \(a > 1\), तो ग्राफ बढ़ रहा है और अवतल है। भी:

चरण 3 : यदि \(0 < a < 1\), तो ग्राफ घट रहा है और उत्तल है। भी:

आसान, है ना??