लॉग नियम
लॉगरिदमिक फ़ंक्शन गणित में सबसे महत्वपूर्ण कार्यों में से एक है, और लॉग नियम सरल और सुविधाजनक हैं, जिससे लॉगरिदम के साथ काम करना वाकई आसान हो जाता है।
आइए पहले याद करें कि \(\log_b a\) का अर्थ क्या है। इस संदर्भ में, मान \(b\) है आधार लघुगणक का, और \(a\) है तर्क .
हम कहते हैं कि \(\log_b a = y\) जब \(b^y = a\)। यह कह रहा है कि \(\log_b a\) वह संख्या है जिसे \(b\) (आधार) को \(a\) (तर्क) प्राप्त करने के लिए ऊपर उठाने की आवश्यकता है।
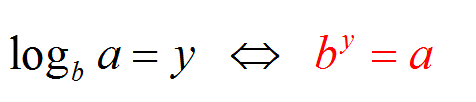
उदाहरण के लिए, \(\log_{10} 25\) उस संख्या से मेल खाता है जिसे 25 प्राप्त करने के लिए मुझे 10 तक बढ़ाने की आवश्यकता है। इसलिए मैं जिस लघुगणक की तलाश कर रहा हूं वह संख्या \(y\) है जिसमें संपत्ति \(10^y = 25\) है।
अब प्रश्न यह है कि हम उस संख्या \(y\) की गणना कैसे करते हैं जिसमें \(10^y = 25\) गुण है? खैर, वह संख्या अच्छी तरह से परिभाषित है, और लॉगरिदमिक फ़ंक्शन \(f(x) = \log_{10} x\) इसका ख्याल रखता है। यह फ़ंक्शन एक प्राथमिक फ़ंक्शन नहीं है, और इसे दर्शाने के लिए एक टेलर सीरीज़ (अनंत श्रृंखला) की आवश्यकता होती है।
या, आप एक कैलकुलेटर का उपयोग कर सकते हैं (जो शायद आसान है, है ना?)
लॉग-नियम: लघुगणक के गुण
ये मुख्य लॉग-नियम हैं:
नियम 1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
नियम #2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
नियम #3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
नियम #4 : \(\large \log_a (a) = 1 \)
नियम #5 : \(\large \log_a (1) = 0 \)
उदाहरण 1
लॉग नियमों का उपयोग करके \(\log_2 8 + \log_2 4\) को सरल बनाएं:
उत्तर:
नियम # 1 का उपयोग करते हुए, हम पाते हैं कि:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]तो, पहला कदम नियम #1 का एक सरल अनुप्रयोग है, लेकिन हम इसे \(\log_2 32 = 5\) कैसे प्राप्त करते हैं? ऐसा इसलिए है क्योंकि \(2^5 = 32\), इसलिए इस मामले में हम सीधे पाते हैं कि \(32\) प्राप्त करने के लिए आपको \(2\) कितनी संख्या बढ़ाने की आवश्यकता है।
अधिकांश लघुगणक की गणना करने के लिए आपको एक कैलकुलेटर की आवश्यकता होगी। यह केवल कुछ चुनिंदा हैं जिन्हें आप सीधे गणना कर सकते हैं। \(\log_{10} 100 = 2\) जैसे सामान, क्योंकि आप आसानी से जानते हैं कि \(10^2 = 100\)।
लेकिन, क्या आप सीधे \(\log_{10} 102\) की गणना कर सकते हैं? वास्तव में नहीं, इसके लिए आपको एक कैलकुलेटर की आवश्यकता है।
उदाहरण 2
लघुगणक का योग और घटाव व्यक्त करें: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \)।
उत्तर:
सबसे पहले, हमें यह याद रखना होगा कि घनमूल लेना \(1/3\) शक्ति को बढ़ाने के समान है। दूसरे शब्दों में, \(\sqrt[3]{x}\) \(x^{1/3}\) के समान है।
तो फिर, हम पहले नियम #3 का उपयोग घात को लघुगणक के सामने लाने के लिए करते हैं, और फिर हम नियम #1 और #2 का उपयोग करते हैं। हम पाते हैं:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]जो आवश्यक था: सरल लघुगणक का योग और घटाव।
लघुगणक के लिए आधार सूत्र का परिवर्तन
लघुगणक से संबंधित सबसे उपयोगी सूत्रों में से एक आधार सूत्र का परिवर्तन है। यह सूत्र इस प्रकार है:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]यह सूत्र केवल यह कह रहा है कि यदि आप आधार को \(b\) से \(c\) में बदलना चाहते हैं, तो परिणाम अनिवार्य रूप से समान हैं, लेकिन आपको नए आधार के लघुगणक से विभाजित करने की आवश्यकता है।
अब, यदि आप कलात्मक रूप से उन्मुख हैं, तो आप नीचे व्यक्त किए गए आधारित सूत्र के परिवर्तन के वैकल्पिक रूप का आनंद ले सकते हैं:
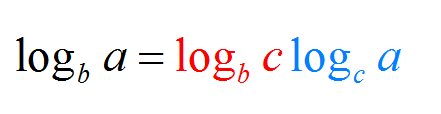
उदाहरण 3
प्राकृतिक लघुगणक \(\ln\) को \(\log\) (आधार 10) के रूप में व्यक्त करें।
उत्तर:
आधार सूत्र के परिवर्तन का उपयोग करते हुए, हम प्राप्त करते हैं:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]तो आप कह रहे हैं कि \(\ln a\) \(\log a\) को \(\log e\) से विभाजित करके प्राप्त किया जाता है। कितना सुविधाजनक? कौन कहता है गणित कठिन था, हुह?
लॉग-नियमों के बारे में अधिक जानकारी
गणित में लघुगणक वास्तव में महत्वपूर्ण हैं। ऐतिहासिक रूप से, चंद्रमा और ग्रहों की गति की भविष्यवाणी करने के तरीके के रूप में, लघुगणक खगोल विज्ञान में बहुत महत्वपूर्ण भूमिका निभाते हैं।
लॉगरिदमिक कार्य गणित में सब कुछ के बीच में स्थित है, यह घातीय, घातांक और बहुत कुछ सब कुछ के साथ परस्पर जुड़ा हुआ है। इसलिए वे आपको दिल से लघुगणक सीखने के लिए कहते हैं, क्योंकि वे महत्वपूर्ण हैं।
साथ ही, यहां प्रस्तुत ये लॉग नियम सुविधा प्रदान करने में महत्वपूर्ण भूमिका निभाते हैं लघुगणक समीकरणों का संकल्प .
संकेतन सम्मेलन
कुछ संकेतन सम्मेलन हैं जिनके बारे में आपको जानना आवश्यक है। सामान्य तौर पर, हम \(\log_b a\) लिखते हैं, और हम इसे "a का लॉग बेस b" कहते हैं। जब आधार \(b = 10\) होता है, तो परंपरा के अनुसार हम केवल \(\log a\) लिखते हैं। तो जब आप बिना आधार के \(\log\) देखते हैं, तो यह माना जाता है कि आधार \(10\) है।
एक और उल्लेखनीय मामला है। \(\log_b a\) के लिए, जब आधार \(b = e\) (यूलर स्थिरांक) है, तो हम \(\log_e a\) के बजाय \(\ln a\) लिखते हैं। इसलिए, जब \(\log\) के बजाय \(\ln\) का उपयोग किया जाता है, तो इसका कारण यह है कि लघुगणक का आधार \(e\) है।
ध्यान दें कि \(\ln a\) को आमतौर पर के रूप में संदर्भित किया जाता है प्राकृतिक लॉग . और हाँ, प्राकृतिक लॉग में सामान्य लॉग के समान नियम होते हैं।
यदि आपके पास एक लॉगरिदमिक फ़ंक्शन है जिसे आप ग्राफ़ करना चाहते हैं, तो आप हमारी कोशिश कर सकते हैं लॉगरिदमिक फंक्शन ग्राफ मेकर , जो आपको एक साफ-सुथरा प्रस्तुत ग्राफ़ प्रदान करेगा।
