क्षैतिज asymptotes
इस ट्यूटोरियल में हम अवधारणा को कवर करेंगे समसthurीय अनंतसchurcurauth rabas और इसके सबसे महत्वपूर्ण अनुप्रयोग।हम किसी भी अति तकनीकी स्पष्टीकरण से बचने की कोशिश करेंगे, लेकिन कैलकुलस के कुछ स्पर्शों का उपयोग किया जाएगा।
ज्यादातर, इस ट्यूटोरियल से बाहर निकलने का महत्वपूर्ण हिस्सा क्षैतिज एसिम्प्टोट्स के बारे में एक मजबूत ज्यामितीय अंतर्ज्ञान है।चलो शुरू करें!
एक क्षैतिज स्पर्शोन्मुख क्या है
एक क्षैतिज स्पर्शोन्मुख एक ऊपरी बाउंड है, जिसे आप एक क्षैतिज रेखा के रूप में कल्पना कर सकते हैं जो किसी दिए गए फ़ंक्शन के ग्राफ के व्यवहार के लिए एक सीमा निर्धारित करता है।
इसका मतलब यह है कि फ़ंक्शन का ग्राफ \(f(x)\) इस क्षैतिज रेखा के दृष्टिकोण के रूप में, \(x\) का मान बढ़ता है।
आप क्षैतिज स्पर्शोन्मुख कैसे पाते हैं?
इस विशेषता को प्रदर्शित करने वाले कार्यों के इस सीमित क्षैतिज व्यवहार को समझना क्षैतिज स्पर्शोन्मुख खोजने के लिए बहुत उपयोगी साबित हो सकता है।
दरअसल, कुछ परिस्थितियों में, यह सीमित व्यवहार \(x\)के बड़े मूल्यों के लिए एक क्षैतिज रेखा की तरह सुंदर लगता है।उदाहरण के लिए नीचे दिए गए फ़ंक्शन को देखें।
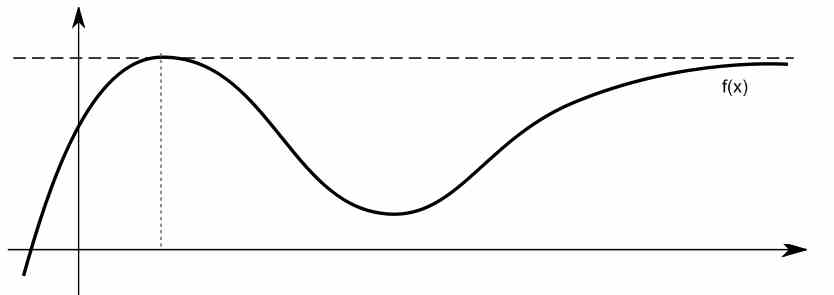
आप किसी फ़ंक्शन के क्षैतिज स्पर्शोन्मुख को सीमाओं का उपयोग करके कैसे पाते हैं?
परिभाषा को स्पष्ट करने के लिए, एक क्षैतिज रेखा \(y = h\) फ़ंक्शन का एक क्षैतिज asymptote है \(f(x)\) यदि
\[\large \lim_{x\to\infty} f(x) = h\]यदि उपरोक्त सीमा मौजूद है और यह परिमित है।उन लोगों के लिए जो अभी तक एक कैलकुलस क्लास से नहीं गुजरे हैं, क्षैतिज रेखा \(y = h\) फ़ंक्शन का एक क्षैतिज asymptote है \(f(x)\) जब \(h\) है आप सीमा \(f(x)\) के रूप में \(x\) अनंत के लिए दृष्टिकोण।"सीमा" होने का क्या मतलब है?इसका मतलब है कि \(x\)के पर्याप्त मूल्यों के लिए, \(f(x)\)का मान \(h\)के करीब होगा क्योंकि हम पूर्वनिर्धारित हैं।फैंसी, सही?
क्षैतिज स्पर्शोन्मुख के लिए सूत्र क्या है?
क्षैतिज स्पर्शोन्मुख के लिए सूत्र खोजने के लिए, हमें पहले संबंधित सीमा को खोजने की आवश्यकता है।मान लें कि आपके पास है
\[\large \lim_{x\to\infty} f(x) = h\]उस स्थिति में, हम कहेंगे कि क्षितिज एसिम्पोटोट \(h\)है, और क्षैतिज asymptote के लिए सूत्र \(y = h\)है।दूसरे शब्दों में, क्षैतिज स्पर्शोन्मुख सरल है क्षैतिज रेखा है, यह ढलान शून्य के साथ एक रेखा है।
यह अर्थ देता है कि सीमा के संदर्भ में एक क्षैतिज स्पर्शोन्मुख का क्या अर्थ है: पाया गया सीमा क्षैतिज रेखा को परिभाषित करने के लिए मेल खाती है जिसे क्षैतिज स्पर्शोन्मुख कहा जाता है।
उदाहरण 1
फ़ंक्शन के लिए एक क्षैतिज asymptote खोजें
\[ \large f(x) = \frac{x^2}{x^2+1} \]उत्तर:
क्षैतिज asymptote को खोजने के लिए, हमें फ़ंक्शन की सीमा \(f(x)\) के रूप में \(x\) अनंत के लिए दृष्टिकोण खोजने की आवश्यकता है।यदि आप कैलकुलस से परिचित नहीं हैं, तो आपको पहले \(x\)के बहुत बड़े मूल्य पर फ़ंक्शन का मूल्यांकन करने का प्रयास करना चाहिए।
उदाहरण के लिए, मान लीजिए कि \(x = 1,000,000\)।आइए हम इस नंबर को फ़ंक्शन में प्लग करें:
\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]जो कि 1 के करीब है, तो तब किसी को संदेह होना चाहिए कि सीमा 1 है। वास्तव में, यह पता चला है कि जब \(x\)बड़ा होता है, तो \(x^2\)का मान 1 के संबंध में इतना बड़ा है, कि \(x^2\)कम से कम सापेक्ष शब्दों में \(x^2 + 1\) के समान है।इसलिए, हमारे पास \(x^2\)द्वारा अंश और भाजक को विभाजित करके है:
\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]क्योंकि \(\frac{1}{x^2}\) 0 के रूप में \(x\) अनंत के लिए दृष्टिकोण करता है।इसलिए, यह साबित करना मुश्किल नहीं है, या आश्वस्त होना चाहिए
\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]जिसका अर्थ है कि क्षैतिज स्पर्शोन्मुख \(y = 1\)है।अब, अपने उत्तर से सावधान रहें यदि आप किसी परीक्षण या होमवर्क का जवाब दे रहे हैं।कुछ लोग कहेंगे "क्षैतिज स्पर्शोन्टोट 1 है", जो गलत है।
तकनीकी रूप से, क्षैतिज एसिम्पोटोट फ़ंक्शन \(y = 1\)है, और संख्या 1 नहीं है। क्षैतिज asymptote एक फ़ंक्शन है जो स्थिर है, जो एक संख्या के समान नहीं है।बस कह रहा है, क्योंकि वहाँ कुछ picky ग्रेडर हैं।
उदाहरण 2
यदि यह फ़ंक्शन के लिए मौजूद है, तो एक क्षैतिज asymptote खोजें
\[ \large f(x) = \frac{x^3}{x^2+1} \]उत्तर:
\(x^2\)द्वारा अंश और भाजक को विभाजित करके:
\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]पर रुको!यहां काम नहीं किया?हाँ इसने किया।ध्यान दें कि भाजक 1 के बहुत करीब हो जाएगा क्योंकि \(x\) बहुत बड़ा हो जाता है, और अंश बहुत बड़ा हो जाएगा।
यह विश्वास करना मुश्किल नहीं है कि \(f(x)\) अनंत में परिवर्तित हो जाता है, ताकि एक क्षैतिज स्पर्शोन्मुख न हो।किसी भी समय हम एक फ़ंक्शन देखते हैं जो अनबाउंड है, जैसे कि यह \(f(x)\) के लिए मामला है, इस उदाहरण में, हमारे पास एक क्षैतिज स्पर्शोन्मुख नहीं होगा।
क्षैतिज asymptote या क्षैतिज asymptotes?
तकनीकी रूप से दो क्षैतिज एसिम्प्टोट्स हो सकते हैं, एक बाईं ओर और एक दाईं ओर।बाएं क्षैतिज asymptote \(y = h_L\) है
\[\large \lim_{x \to -\infty} f(x) = h_L\]इसी तरह, सही क्षैतिज asymptote \(y = h_R\) है
\[\large \lim_{x \to +\infty} f(x) = h_R\]इस मामले में कि उपरोक्त सीमाओं में से कोई भी मौजूद है, और परिमित हैं।यह हो सकता है कि एक फ़ंक्शन में दो क्षैतिज स्पर्शोन्मुख होते हैं, इसमें केवल एक क्षैतिज स्पर्शोन्मुख होता है, या इसमें कोई भी नहीं होता है।
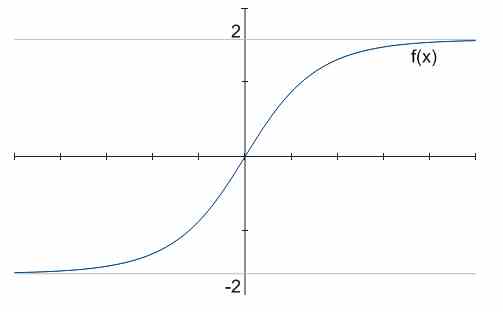
उदाहरण के लिए, ऊपर के ग्राफ में, दो क्षैतिज asymptotes, \(y = -2\)और \(y = 2\)हैं।
क्षैतिज स्पर्शोन्मुख खोजने के लिए नियम क्या है?
कोई सामान्य नियम नहीं हैं जो सभी मामलों के लिए काम करेंगे।सामान्य मामले में हमें \(x\)के रूप में \(-\infty\)के दृष्टिकोण के रूप में सीमा की गणना करने की आवश्यकता है, और \(x\)के रूप में सीमा \(+\infty\)पर पहुंचती है।
यदि उन सीमाओं में से कोई भी मौजूद है और परिमित हैं, तो हमारे पास क्षैतिज स्पर्शोन्मुख होंगे।
एक विशिष्ट नियम इस मामले के लिए तैयार किया जा सकता है कि दिया गया फ़ंक्शन \(f(x)\) दो बहुपदों का भागफल है।यदि वह मामला है, तो हमें यह मानने दें कि \(m\) अंश में बहुपद का क्रम है, और \(n\) हर में बहुपद का क्रम है।फिर हमारे पास निम्नलिखित मामले हैं:
तंगा यदि \(m < n\), तो क्षैतिज asymptote \(y = 0\)है।
केस 2: यदि \(m = n\), और \(a\)अंश में बहुपद के लिए अग्रणी गुणांक है, और \(b\)भाजक में बहुपद के लिए अग्रणी गुणांक है, तो क्षैतिज स्पर्शोन्मुख \(\displaystyle y = \frac{a}{b}\)है।
केस 3: यदि \(m > n\), तो कोई क्षैतिज स्पर्शोन्मुख नहीं है।
उदाहरण 2
खोजें, यदि मौजूद है, तो फ़ंक्शन का क्षैतिज स्पर्शोन्मुखी
\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]उत्तर:
फ़ंक्शन में दो बहुपदों के भागफल होते हैं।अंश में बहुपद \(3x^2+2x-1\)है, जो ऑर्डर 2 का एक बहुपद है, इसलिए फिर \(m = 2\), और अग्रणी गुणांक 3।
हर में बहुपद \(2x^2 -x+2\)है, जो ऑर्डर 2 का एक बहुपद है, तो फिर \(n = 2\), और अग्रणी स्थिर 2. आप हमारा उपयोग कर सकते हैं बहुपद कैलकुलेट इस डिवीजन का संचालन करने के लिए सभी चरणों को दिखाते हुए।
इसलिए, चूंकि इस मामले में \(m = n\), एक क्षैतिज स्पर्शोन्मुख है, और यह प्रमुख गुणांक का भागफल है, इसलिए फिर इस मामले में, क्षैतिज स्पर्शोन्मुख है
\[\large y = \frac{3}{2}\]क्षैतिज asymptotes के बारे में अधिक
तो आपका सवाल यह है कि आप एक समीकरण के एसिम्प्टोट्स को कैसे पाते हैं, है ना?सबसे पहले, आप a के asymptotes पाते हैं तमाम , एक समीकरण का नहीं।फिर, आपको सीमाओं का उपयोग करके सामान्य परिभाषा के साथ शुरू करने की आवश्यकता है।
यदि आप कैलकुलस नहीं जानते हैं और सीमा की गणना कैसे करें, तो नहीं जानते हैं, तो आपको कम से कम \(x\)के बहुत बड़े मानों को प्लग करने की कोशिश करनी चाहिए, और फ़ंक्शन पर \(x\)के बहुत नकारात्मक मान भी चाहिए, और देखें कि कैसेकार्य व्यवहार करता है।
यहां तक कि कुछ सॉफ़्टवेयर के साथ फ़ंक्शन की साजिश रचने से आपको एक स्पष्ट संकेत मिल सकता है यदि क्षैतिज एसिम्प्टोट्स हैं।
अंततः, बहुत प्रतिबंधित मामले में जिसमें फ़ंक्शन एक है अँगुला , फिर आप आदेश \(m\)और \(n\)के आधार पर नियम लागू कर सकते हैं।
अलग -अलग डिग्री के साथ क्षैतिज एसिम्प्टोट्स कैसे खोजें?
वे विभिन्न प्रकार के एसिम्प्टोट्स हैं, और उन्हें तिरछा एसिम्पोटोट कहा जाता है।हम एक और ट्यूटोरियल में तिरछा asymptotes के बारे में बात करेंगे।
