حساب التفاضل والتكامل دروس

طريقة الاستبدال للتكامل

طريقة الاستبدال للتكامل أو التكامل من خلال طريقة الاستبدال هي تقنية ذكية وبديهية تستخدم لحل الأكياد, ولعب دورا حاسما في واجب حل الأكاديات, إلى جانب تكسل اجزاء و تحلل الكسور الجزئية طريقة.

يمكن أن يكون التكامل عملية صعبة في بعض الأحيان, ولنا فقط عدد قليل من الأدوات المتاحة للمتابعة.

بطبيعة الحال, فإن حساب جزء لا يتجزأ من غير مسمى لبعض الوظائف الأولية الأساسية (مثل متعدد الحدود, والقوى, والوظائف المثلثية الأولية, إلخ) بسيط للغاية.

ولكن السؤال هو كيفية المضي قدما في حساب التكامل غير المحدود (أو البدائي) لأكثر تعقيدا أو لمجموعة الجبرية من الوظائف.

هل أنت على استعداد لموسيقى الروك؟؟أنا, لذلك اتبعني.

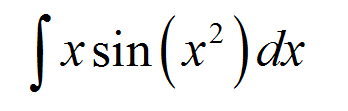
كيف تعمل طريقة الاستبدال؟

تعمل طريقة التكامل عن طريق الاستبدال عن طريق تحديد "كتلة" تحتوي على متغير التكامل, بحيث يمكن أيضا العثور على مشتق هذا الكتلة داخل جزءا لا يتجزأ.كما تسمى هذه الطريقة أيضا طريقة استبدال U.

إذا سمح بنية التكامل, يصبح "الكتلة" هذه في الواقع متغير تكامل جديد, إذا كان كل شيء على ما يرام, ويصبح التكامل مبسرا بشكل خطير.

هل يعمل دائما؟لا. أو قال بشكل مختلف, يمكنك دائما إجراء استبدال, لكنه لن يحوله دائما إلى جزء أسهل.

لماذا حتى جرب هذه الطريقة؟حسنا, لأنه يعمل في كثير من الأحيان.وعادة ما تكون هناك خدعة أول يجب أن تحاول أن تحاول حل جزء لا يتجزأ غير تافهة.

دعونا نضع بضع خطوات لمتابعة إذا كنت بحاجة إلى تطبيق هذه الطريقة:

الخطوة 1: فحص الوظيفة التي تدمجها والبحث عن "كتلة", هذا هو, وظيفة \(x\) التي تظهر مرة واحدة أو أكثر في الوظيفة التي تدمجها.

الخطوة 2: يحتاج "كتلة" التي تبحث عنها للحصول على خاصية محددة للغاية: يحتاج مشتق الكتلة إلى الظهور مرة واحدة ومرة واحدة فقط في الوظيفة التي يتم دمجها.

الخطوه 3: إذا كانت الخطوات السابقة ناجحة, فيمكنك استخدام "كتلة" كمتغير جديد, ويمكنك استبدال المتغير والتفاضل إلى المتغير الجديد, والتكامل التي تحلها أصبحت الآن أكثر بساطة.

ملاحظة تقنية : عادة ما أحاول الحفاظ على جميع التفسيرات بسيطة, وحاول تجنب التقنيات.في هذه الحالة, سيتعين علي إعطاء التفسير الفني لطريقة الاستبدال, وعدم ترك الأمور غير رسمية للغاية بفكرة "كتلة".

إذا كنت لا تحب التقنيات, فيمكنك تخطي إلى القسم التالي, حيث سترى الأمثلة.

لذلك, فإن الفكرة بأكملها هي دمج وظيفة معينة \(f(x)\).لذلك نحن بحاجة إلى العثور على:

\[\int f(x) \, dx\]

قل أن وظيفة \(f(x)\) ليست مجرد أي وظيفة, ولها هيكل معين معين, وتحديدا

\[f(x) = g(h(x))h'(x)\]

ونفترض أن هناك وظيفة \(G(x)\) بحيث \(G'(x) = g(x)\) (لذلك ثم \(G\) هو مضاد المضاد \(g\)).بعد ذلك, نحصل على ذلك

\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]

لماذا هذا؟؟؟ حسنا, بسيطة: بحكم التعريف, مضاد المضاد هو وظيفة بحيث تكون عند التمييز عليه, تحصل على الوظيفة التي تدمجها.

في هذه الحالة, إذا قمت بالتمييز \( G(h(x)) \) تحصل عليه

\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]

بحكم السلسلة ..... وشمازام!لديك.أخبرتك أنه لم يكن ذلك صعبا.

أمثلة على طرق الاستبدال

أفضل طريقة للذهاب في تعلم كيفية الاندماج هو ممارسة.سيفرح بعض الأشخاص بالنظر إلى البراهين, لكن غالبية الناس سوف يرغبون في رؤية الأشياء في الممارسة العملية.

لذلك, دعونا ننتقل إلى أسباب عملية.

مثال 1

العثور على ما يلي غير مسمى لا يتجزأ:

\[\int x \sin(x^2)\,dx\]

إجابه:

وفقا للخطوة 1, نحن نبحث عن كتلة, كتلة محددة جدا.إذا نظرت إلى Integral, فإن متغير التكامل هو \(x\).

هناك الكثير من التجربة والخطأ, يحتمل, عند استخدام هذه التقنية.قل أننا نعتبر الكتلة التالية:

\[u = x^2\]

نحن نعلم أن هذه الكتلة جيدة لأن مشتقاتها \(u' = 2x\), والتي تظهر في التكامل.

ولكن بعد ذلك تقول "أرى \(x\) لكنني لا أرى 2".حسنا, ليست هناك حاجة إلى أن تكون محتملة.يمكننا أن نفعل خدعة.لاحظ ان

\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]

من أنت, ماندريك الساحر ؟؟نكت جانبا, أن الخدعة الصغيرة تعمل.لذلك, استبدال الكتلة هو

\[u = x^2\] \[du = 2x \, dx\]

(تدوين \(du = 2x \, dx\) غير مؤسس وغير صحيح من الناحية الفنية, ولكن لديها أساس متين, لذلك تحمل معها).لذلك جعل هذا الاستبدال يحول التكامل إلى

\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]

لذلك, بمجرد أن تغيرت إلى المتغير الجديد \(u\), أصبح التكامل في أسهل في حل جزء من \(\sin(u)\).بمجرد حلها, يجب أن تتذكر أن تعود إلى المتغير الأصلي.

مثال 2

الآن, دعونا ننتقل إلى مثال أكثر تعقيدا قليلا.حساب التكامل غير المحدد

\[\int e^{x+e^x} \,dx\]

باستخدام طريقة استبدال U.

إجابه:

ما هذا تقول ؟؟؟حسنا, ليس هذا صعبا.لاحظ أنه يمكن إعادة كتابة التكامل غير المحدد على النحو التالي:

\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]

لذلك, الآن أن ترى الشكل الجديد من الوظيفة التي تدمجها, هل يمكنك التوصل إلى "كتلة" أو "استبدال U-"؟

تذكر, لا تخجل من إجراء المحاكمة والخطأ.إذا كان هناك شيء لا يعمل, جرب شيئا آخر.ماذا لو حاولت \(u = e^x\)؟

مشتق الكتلة هو \(u' = e^x\), الذي تم العثور عليه مرة واحدة في الوظيفة الأصلية.وعلاوة على ذلك:

\[u = e^x\] \[du = e^x \, dx\]

لذلك نحصل على:

\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]