صيغة مرونة القوس للجدول

تسمح لك صيغة مرونة الطلب القوسية بتقدير المرونة عند النقاط المعطاة في جدول الطلب, دون الحاجة إلى وجود صيغة صريحة لدالة الطلب.

ما تحتاج إلى توفيره هو جدول يحتوي على عمود للسعر وعمود للكمية المطلوبة. بمجرد كتابة ذلك أو لصقه في جدول البيانات المقدم, سوف تنقر على "حساب" للحصول على مرونة القوس المقابلة التي تم حسابها لك.

لاحظ أن هذا مجرد تقريب: الوضع المثالي هو حساب المرونة باستخدام دالة الطلب , باستخدام المشتقات.

خطوات استخدام مرونة القوس للجدول

ال صيغة مرونة القوس يكون:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

ويمكن تطبيق ذلك على النقاط المتتالية في جدول الطلب. ستتبع الخطوات التالية:

• الخطوة 1: قم بترتيب قيم السعر (P) والكمية المطلوبة (Q) بشكل صحيح
• الخطوة 2: يمكنك إنشاء أعمدة لـ Q2 - Q1, وP2 - P1, وQ1 + Q2, وP1 + P2 إذا كنت تريد جعل الحسابات أكثر وضوحًا, أو يمكنك حساب الصيغة مباشرةً
• الخطوه 3: ستكون هناك نقطة واحدة متخطية في الجدول, حيث تأخذ مرونة القوس نقطة على الجدول والنقطة التي تليها مباشرة في الجدول

إن استخدام تقريب مرونة القوس هذا سيوفر لك صورة ممتازة عن حساسية تغيرات الأسعار للسلعة المحددة التي يتم تحليلها, على الرغم من أنها مجرد تقريب.

كلما زادت نقاط الطلب لدينا, كان التقريب أفضل, خاصة إذا كانت نقاط السعر هذه متقاربة مع بعضها البعض.

ماذا يقيس مرونة القوس؟

تهدف مرونة القوس إلى توفير تقريب للمرونة الحقيقية عند نقطة معينة. يتم حساب المرونة الفعلية من منحنى الطلب من خلال:

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

قد يزعم البعض أن المرونة القوسية ليست أكثر من تقريب, فكيف إذن لها أي قيمة؟ والإجابة على هذا السؤال هي أنه بالنسبة لتحليل المرونة, وتحليل الحساسية في الاقتصاد بشكل عام, فإننا نهتم أكثر بالمدى وليس بنقاط محددة للغاية.

في الواقع, لأغراض الاقتصاد الجزئي, من المفيد أن نعرف ما إذا كنا في نطاق غير مرن أم لا, بدلاً من القيمة المحددة للغاية للمرونة

لا يعني هذا أن القيمة المحددة ليست مهمة, حيث من الجيد أن يكون لدينا هذه القيمة, ولكن مرونة القوس غالبًا ما تكون تقريبًا جيدًا, وسوف تعطينا تمثيلات دقيقة للغاية لنوع نطاق المرونة الذي نواجهه.

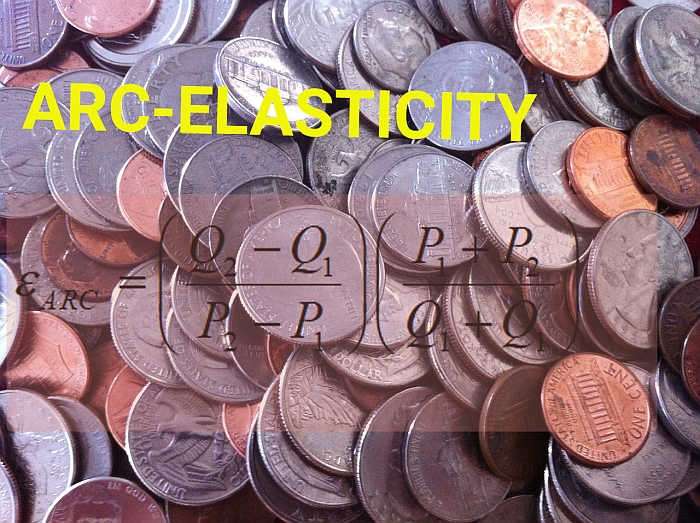
مثال

ضع في اعتبارك جدول الطلب التالي الذي يحتوي على معلومات حول السعر والكمية المطلوبة

توفير تقريب مرونة القوس لنقاط البيانات في هذا الجدول.

ص	س
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

حل: من أجل تقريب مرونة الطلب السعرية من هذه البيانات, نحتاج إلى استخدام صيغة المرونة القوسية التالية

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

من خلال تطبيق الصيغة أعلاه على جميع أزواج نقاط البيانات المتتالية, نجد مرونة القوس التالية:

ص	س	مرونة القوس
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

تفسير

يوضح الجدول الموجود مرونة الطلب السعرية التقريبية لكل نقطة سعرية مقدمة. ويمكن استخدام هذه القيم تقريبًا لتحديد النطاقات المرنة وغير المرنة لجدول الطلب المقدم.

حاسبات اقتصادية أخرى

إذا كنت تعمل في مجال القياس الاقتصادي, فهذا حاسبة الانحدار من المرجح أن يكون مفيدًا, خاصةً لأنه يوضح جميع خطوات عملية حساب معاملات الانحدار .

يمكنك أيضًا استخدام معادلة لوغاريتمية لتقدير منحنى الطلب مع مرونة ثابتة .