النسبة المئوية الحاسبة

هذا النسبة المئوية الحاسبة يمنحك طريقة سريعة لإجراء حساب النسبة المئوية عن طريق توفير الأرقام التي تحتاج إلى استخدامها والنقر فوق زر الحساب

الآن, إذا كنت تريد القيام بذلك يدويًا, فإن حساب النسبة المئوية لرقم \(D\) من رقم آخر \(X\) أمر بسيط للغاية, ويتضمن بعض العمليات الأولية.

كيف يمكنك حساب النسبة المئوية؟صيغة النسبة المئوية

كثيرًا ما يسأل الطلاب "كيف يمكنني حساب النسبة المئوية", والإجابة بسيطة للغاية.نقوم بحساب النسبة المطلوبة ببساطة باستخدام الصيغة التالية:

\[\text{Percentage} = \displaystyle\frac{D}{X} \times 100\]

الأمر بهذه البساطة. خذ قيمة الرقم \(D\) واقسمها على \(X\). ثم اضرب نتيجة هذه القسمة في 100 لتحصل على النسبة المئوية المطلوبة. وقد ترغب في تقريب هذا الرقم إلى أقرب منزلتين عشريتين عادةً.

بمعنى آخر, لديك الجزء (D) مقسومًا على الإجمالي (X).الضرب في 100 له تأثير تسوية الناتج, بحيث تكون النسبة المئوية للمجموع بالنسبة لنفسه 100%.

ما عليك فعله للعثور على نسبة مئوية لبياناتك

• الخطوة 1: حدد بوضوح الجزء (د) والإجمالي (س) الذي تعمل به
• الخطوة 2: إذا كانت هذه الكميات تحتوي على وحدات (متر, أونصة, إلخ), فتأكد من استخدام وحدة مشتركة لها
• الخطوه 3: يمكنك ببساطة حساب النسبة المئوية باستخدام الصيغة التالية: \(\text{Percentage} = \displaystyle\frac{D}{X} \times 100\)

لاحظ أنه إذا كانت الكميات لها وحدات, فيجب التأكد من أنها تستخدم وحدة مشتركة. على سبيل المثال, إذا سألتك "ما النسبة المئوية لـ 30 سم من 2 متر؟", فيمكننا أن نقول إن الجزء هو X = 30, والإجمالي هو D = 2, ومن ثم يمكننا عن غير قصد حساب النسبة المئوية كـ \(\text{Percentage} = \displaystyle\frac{30}{2} \times 100 = 1500 %\).

ما هو الخطأ في هذا الحساب؟الوحدات, يستخدمون وحدات مختلفة.وباستخدام السنتيمترات لكليهما, نجد أن الجزء يساوي 30 سنتيمترًا والمجموع 2 متر, أو 200 سنتيمتر.وبالتالي فإن النسبة الفعلية هي \(\text{Percentage} = \displaystyle\frac{30}{200} \times 100 = 15 %\).

هل هذه هي الطريقة لحساب النسبة المئوية بين رقمين؟

بالضبط! بالضبط كما تم شرحه في الجزء السابق, عليك أن تقسم الجزء (D) على المجموع (X). الآن, عندما يكون لديك رقمين, فإن أحدهما يلعب دور الجزء والآخر هو المجموع.

وبعبارة أخرى, عندما يكون لديك رقمين, عليك حساب نسبة رقم واحد إلى الآخر , والترتيب الذي تختاره مهم.هذا هو, عندما يكون لديك رقمين \(A\) و \(B\), هناك شيء واحد هو نسبة \(A\) بالنسبة إلى \(B\) وهي ليست نفس النسبة المئوية لـ \(B\) بالنسبة إلى \(A\)

ما هو 15 في المئة كرقم؟

من صيغة حاسبة النسبة المئوية, نقوم أولًا بالقسمة ثم نضرب في 100. ثم, بشكل عكسي, للحصول على 15 بالمائة كرقم, علينا قسمة 15 على 100, إذن, 15 بالمائة = 0.15.

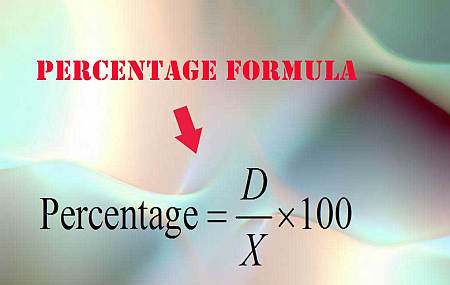
كيف يمكنك الحصول على 40٪ من 80؟

مشابهة جدا للجزء السابق.من أجل إيجاد نسبة مئوية من رقم, نكتب النسبة المئوية في صورة رقم.في هذه الحالة, 40 بالمائة هي نفسها 40/100 = 0.40 كرقم.

وبعد ذلك, لكي نحصل على 40% من 80, نضرب فقط 0.40*80 = 32. وينطبق هذا الأساس المنطقي على جميع المسائل من نفس النوع.على سبيل المثال, بالنسبة لـ 15% من 100, نحصل على 15% كرقم يساوي 15/100 = 0.15, إذن 15% من 100 هي 0.15*100 = 15.

كيفية حساب النسبة المئوية لعدد

خطوات حساب النسبة المئوية لرقم بسيطة:

• الخطوة 1: حدد بوضوح الرقم X, والنسبة المئوية p% التي تريد كمبيوترها
• الخطوة 2: الآن, أنت بحاجة إلى تحويل النسبة المئوية إلى رقم, ولهذا تقسم p على 100. على سبيل المثال, إذا كانت p = 85%, فستحصل على p = 85/100 = 0.85
• الخطوه 3: أخيرًا, النسبة المئوية للرقم الذي تبحث عنه يتم الحصول عليها بسهولة عن طريق ضرب p (كرقم) في الرقم, لذلك هذا هو p*X

مثال على حاسبة النسبة المئوية

مثال: ما هي النسبة المئوية 13 من 38؟

باستخدام الصيغة أعلاه نحصل على:

\[\text{Percentage} = \displaystyle\frac{13}{38} \times 100\] \[ = 0.342105263 \times 100\] \[ = 34.21 \%\]

هل هذا مرتبط بآلة حاسبة النسبة المئوية؟

بالتأكيد, هذا مرتبط جزء الحوسبة إلى نسبة مئوية .بطريقة ما, هو نفس الشيء.في الواقع, كل ما نقوم به في هذه الحالة هو التحقق من الكسر \(\frac{D}{X}\) كنسبة مئوية.

أو بمعنى آخر, حساب النسبة المئوية لـ \(D\) من \(X\) هو نفس حساب النسبة المئوية النسبة المئوية تتوافق مع الكسر \(\frac{D}{X}\).