代数教程

高斯消元法

高斯消元是对矩阵进行的一个过程,旨在将矩阵放入梯形 .拥有这种形式的矩阵对于非常容易地求解矩阵方程非常有帮助。

从技术上讲,进行高斯消元的过程包括找到一个带有主元的列（这是非零元素的花哨俚语）,它允许我们消除主元下方的所有元素。

这个寻找主元和消除的过程允许我们将矩阵放入梯形形式,该过程的方式是通过旋转向梯形形式添加一个新列,并且您不会“破坏”梯形形式已经完成了上一步。如果你问我,很漂亮。

通过查看上面的矩阵,使用高斯消去法获得的术语“梯形形式”变得清晰,其中矩阵的非零元素具有这种梯形结构,如红线所示。

旋转和高斯消元背后的数学

我们不会在这方面过于技术化,我们只会尝试让您了解这种消除的动机和机制。

这个想法是将维度为 \(m \times n\)（即它具有 \(m\) 行和 \(n\) 列）的矩阵 \(A\) 转换为更适合求解方程的不同形式。

更具体地说,对于 \(m\times n\) 矩阵 \(A\) 和 \(m\times 1\) 向量 \(b\),我们需要找到一个 \(n\times 1\) 向量 \(x\) 使得

\[Ax = b\]

您可能会想,“这太简单了,我们只需从左边将每一边乘以 \(A^{-1}\)”,我们得到：

\[x = A^{-1} b \]

....没那么快！这仅在矩阵 \(A\) 可逆时才有效。首先,矩阵 \(A\) 必须是方阵,然后,其行列式需要不为零。但是您不能乘以非方阵的逆矩阵。那么,你怎么做呢？

您需要将方程转换为更容易求解的方程。

具体来说,梯形矩阵是导致方程易于求解的矩阵（稍后会详细介绍）。

使用初等矩阵

首先,我们将做一个重要的笔记。如果我们有矩阵方程 \(Ax = b\) 的解,而 \(E\) 是可逆矩阵,那么 \(x\) 也是 \((EA)x = Eb\) 的解,反之亦然。

换句话说,矩阵方程

\[Ax = b\]

和

\[(EA)x = Eb\]

是等价的,对于可逆矩阵 \(E\)。我们所说的等式是等价的是什么意思？我们的意思是方程有相同的解。

所以我们要做的是从 \(Ax = b\) 开始,通过乘以可逆矩阵 \(E\),我们将得到一个等效的矩阵方程,即 更容易解决 .

假设我们能够找到一个可逆矩阵列表 \(E_1, E_2, ..., E_n\) 并且我们（从左边开始）乘以原始矩阵方程以将其转换为等效方程,例如：

\[Ax = b \,\,\,\, \Leftrightarrow \,\,\,\, (E_1 \cdot A)x = (E_1 \cdot b)\] \[... \Leftrightarrow \,\,\,\, (E_n \cdots E_2 \cdot E_1 \cdot A)x = (E_n \cdots E_2 \cdot E_1 \cdot b)\] \[ \Leftrightarrow \,\,\,\, \tilde A x = \tilde b\]

其中 \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) 和 \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\)。

我们的宗旨是认真选择可逆矩阵 \(E_1, E_2, ..., E_n\) 使 \(\tilde A\) 处于梯形形式。

这是为什么？因为如果 \(\tilde A\) 是梯形的,求解矩阵方程 \(\tilde A x = \tilde b\) 就容易多了,而且我们已经知道 \(\tilde A x = \tilde b\) 和 \(A x = b\) 有相同的解

例 1

让我们看看为什么当您以梯形形式求解矩阵方程时会容易得多。首先假设您有以下矩阵和向量：

\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & -1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]

并且您想解决 \(Ax = b\)。方程组会是什么样子？系统 \(Ax = b\) 看起来像

\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 - x_3 = 1\]

它看起来如何？嗯,不是那么整洁。您需要开始处理方程式。有或多或少的系统方法可以使用消除等方法来解决这个问题,但这至少很麻烦。

现在,另一方面,假设您有以下矩阵和向量：

\[\tilde A = \left[ \begin{matrix} -1 & 1 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{matrix} \right] \] \[\tilde b= \left[ \begin{matrix} 1 \\ -1 \\ -1 \\ \end{matrix} \right]\]

并且您想解决 \(\tilde A x = \tilde b\)。在这种情况下,矩阵 \(\tilde A\) 是梯形的。方程组会是什么样子？系统 \(\tilde A x = \tilde b\) 看起来像

\[-x_1 + x_2 + x_3 = 1\] \[x_2 - x_3 = -1\] \[x_3 = -1\]

这个怎么看？嗯,不是太寒酸。

事实上,如果我们直接从第三个方程开始,我们就直接得到了 \(x_3 = -1\)。然后从第二个方程,\(x_2 = -1 + x_3 = -1 + (-1) = -2\)。从第一个方程,\(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\)。所以没有任何模糊,我们发现：

\[x_1 = -4, \, x_2 = -2, x_3 = -1\]

因此,在这种情况下,系统很容易解决。

对于与梯形矩阵相关联的系统,可以直接从最后一个方程回溯到第一个方程以获得解。

如何选择正确的可逆矩阵

现在我们知道使用梯形矩阵可以更容易地求解矩阵方程,我们应该想知道什么是可逆矩阵 \(E_1, E_2, ..., E_n\) 可以使 \(\tilde A\) 成为梯形。

高斯消元如何工作？

有趣的是,不难找到这些矩阵 \(E_1, E_2, ..., E_n\),它们将被称为初等矩阵。

第1步 ：看第一列,如果它有一个非零值,那将是你的枢轴。如果第一列的第一行非零,则将其用作枢轴。如果不是,请找到具有非零值的行并置换该行和第一行。

所以,你找到了一个主元,可能你需要做一个行置换（这实际上是通过乘以某个可逆矩阵来表示的）

第2步 ：一旦你有了一个枢轴,消除当前列中枢轴下方的所有元素。

这是通过将枢轴行乘以某个常数,并将其添加到枢轴下方的行中来完成的,这样与枢轴在同一列中的元素为零。

第 3 步 ：一旦通过适当的行操作（恰好由可逆矩阵的操作表示）使枢轴下方的所有元素都为零后,移动到下一列,下一行,并从下面的行中寻找枢轴前一个枢轴的行并进行相同的程序。

第四步 : 重复直到列用完或矩阵呈梯形。

例2

使用旋转和高斯消元法,求解以下系统：

\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 + x_3 = 1\]

回答：

首先,关联矩阵 \(A\) 和向量 \(b\) 是：

\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & 1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]

增广矩阵 \([A|b]\) 是

\[\left[ \begin{matrix} 1 & 1 & 1 & 2 \\ 1 & -1 & 1 & 1 \\ -1 & 1 & 1 & 1 \\ \end{matrix} \right]\]

为了求解系统,我们需要进行高斯消元。我们选择第一个枢轴,从第一列开始。第一列的第一行的元素为1,它不同于零,然后用作枢轴。我们使用枢轴 (1) 来消除其下方的所有元素：

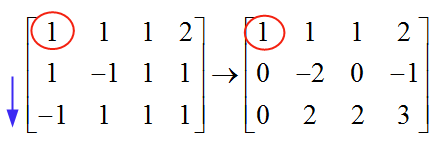
消除枢轴下方元素的机制很简单。在这种情况下,为了消除枢轴下方的“1”,我将第 1 行中的元素减去第 2 行中的元素。这样我在枢轴下形成了一个零。

类似地,为了消除第 3 行中的“-1”,我将第 1 行中的元素添加到第 3 行中的元素。这样我在第 3 行中的枢轴下形成了一个零。

我们将看到这个行操作是通过乘以可逆矩阵来实现的,因此我们通过这样做得到了等价的系统。

现在,移至下一行,下一列,我们找到一个不同于零的“-2”,因此,它被用作我们的枢轴。为了消除该枢轴下方的值,我们将第 2 行的值添加到第 3 行：

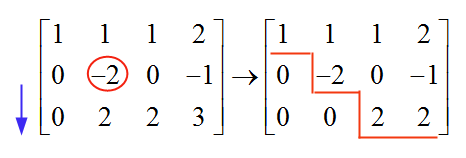
现在我们停止,因为结果矩阵已经是梯形的了。现在我们回溯解决系统：

\[2x_3 = 2 \,\,\,\, \Rightarrow \,\,\,\, x_3 = 1\] \[-2x_2 = -1 \,\,\,\, \Rightarrow \,\,\,\, x_2 = 1/2\] \[x_1+x_2+x_3 = 1 \,\,\,\, \Rightarrow \,\,\,\, x_1 = 1 - x_2 - x_3 = 1 - 1/2 - 1 = -1/2\]