克莱默法则
Cramer's Rule 是一种基于行列式计算系统地求解线性方程组的技术。
通常,求解 线性方程组 对于大于 2x2 的系统来说可能会很混乱,因为当有三个或更多变量时,有很多方法可以减少它。
Cramer's Rule 提供了一种明确的,系统的方法来寻找线性方程组的解,而不管系统的大小。
对于大型系统,所需的计算次数确实会增加,但无论系统大小如何,过程都完全相同。
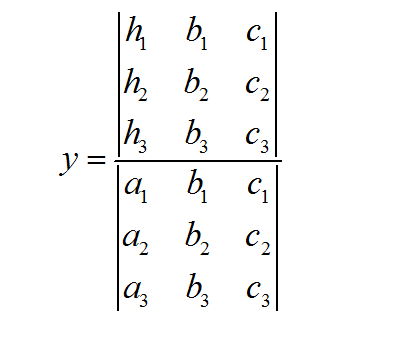
如何使用克莱默规则
为了使事情更容易,我们将制定 \(n = 2\) 的案例,然后我们将建立一个更通用的版本,希望在处理 \(n=2\) 案例后更有意义。
第1步
：所有 2x2 线性系统都可以写成以下形式：
那么你的第一步是为你想要解决的系统找到这些值 \(a_1, b_1, c_1\) 和 \(a_2, b_2, c_2\) 。
第2步
：一旦你有了 \(a_1, b_1, c_1\) 和 \(a_2, b_2, c_2\) 系数,你就可以使用以下公式来求解 \(x\) 和 \(y\)：
在上面的公式中,“det”表示对应矩阵的行列式。有时,行列式使用更紧凑的符号,如下所示：
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]因此,使用上面的符号,我们将得到这些更紧凑的 Cramer 规则公式：
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]让我们以一种直观的方式来理解正在发生的事情。观察到 \(x\) 和 \(y\) 在分母中具有相同的行列式。
分母中使用的公共矩阵的系数直接从系统中乘以 \(x\) 和 \(y\) 的系数推导出来。见下图：
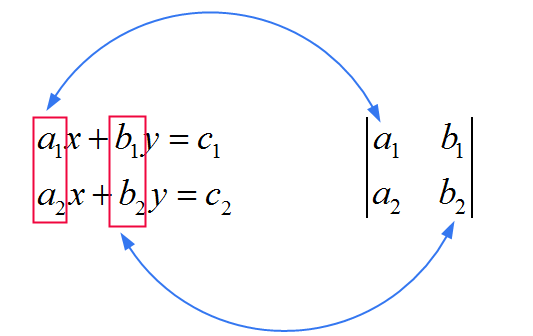
现在我们看到 \(x\) 和 \(y\) 在分子中的不同。作为记住规则的一种方式,请考虑以下内容：
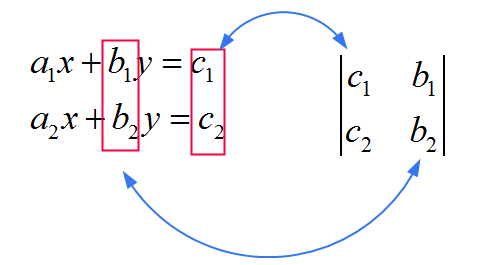
对于 \(x\),您使用 SAME 矩阵作为分母中的矩阵,只是将第一列替换为系数 \(c_1\) 和 \(c_2\)。见下图
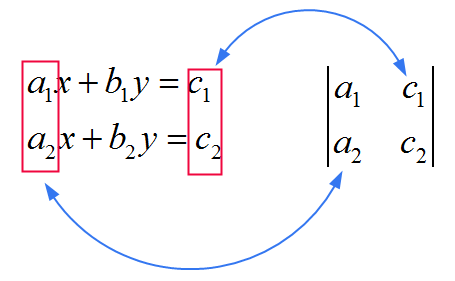
对于 \(y\),您使用 SAME 矩阵作为分母中的矩阵,只是您将 SECOND 列替换为系数 \(c_1\) 和 \(c_2\)。见下图
例 1
求解以下 2x2 线性系统：
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]回答：
让我们按照上面描述的两个步骤使用 Cramer 规则来解决上面的系统：
第1步
：我们需要确定相应行列式的系数。
对于进入分母的矩阵,我们使用
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]现在,在这种情况下 \(c_1 = 10, c_2 = 4\),对于用于计算 \(x\) 的行列式,我们通过更改第一列来替换之前的矩阵：
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]对于用于计算 \(y\) 的行列式,我们通过更改 SECOND 列来替换之前的矩阵：
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]所以现在我们得到了解决方案：
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]对于 \(y\)：
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]因此,解是\(x = 3\),\(y = 1/2\)。
Cramer 的一般情况规则
Cramer 规则的美妙之处在于它应用完全相同的程序,无论是 2x2 系统还是 10x10 系统。这个概念是一样的。
因此,假设 \(x_1, x_2, ..., x_n\) 是变量（未知数）,我们要求解以下 nxn 线性方程组：
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]为了求解 \(x_1, x_2, ..., x_n\),我们将在分母上使用以下行列式：
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• \(x_1\) 的解是
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• \(x_2\) 的解是
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]等等。如您所见,分母中的行列式是相同的,分子中的行列式是通过将第一列更改为 \((c_1, ..., c_n)\) 为 \(x_1\) 得到的。对于 \(x_2\),我们将第二列更改为 \((c_1, ..., c_n)\),对于 \(x_3\),我们将第三列更改为,依此类推。你明白了。
例2
使用克莱默规则求解以下 3x3 线性方程组。
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]回答：
首先,我们确定分母中的行列式：
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]此外,我们需要确定 \(c_i\) 系数的向量：
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]该向量将替换来自分母的公共行列式的相应列。我们得到：
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]更多关于克莱默规则
Cramer 法则在有效求解线性方程组方面具有特定作用。它涉及使用决定因素来使一项非常简单的任务变得非常简单,否则会非常复杂,尤其是对于较大的系统。
最终,为了 求解线性系统 ,你所要做的就是根据需要求解的系统确定一个数矩阵行列式,并进行简单的代数运算来求解该系统。
应用
Cramer 法则在线性代数和微分方程中都有许多应用。