集成替代方法
通过替代方法的集成或集成的替代方法是用于解决积分的聪明而直观的技术,并且在解决积分的责任中起着至关重要的作用,以及 零零一体化 和 部分级分键 方法。
集成可能是困难的操作,并且我们只有几个可用于继续的工具。
当然,对某些基本基本功能的无限积分（例如多项式,电力,基本三角函数等）的计算非常简单。
但问题是如何继续计算用于更复杂的功能或用于函数的代数组合的无限积分（或原始）。
你准备好摇滚吗？我是,所以跟着我。
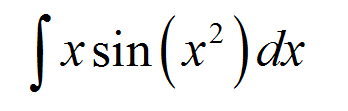
替代方法如何工作？
通过识别包含积分变量的“块”来实现通过替换的方法,从而可以在积分内部找到该块的导数。该方法也通常称为U替代方法。
如果积分允许的结构,则此“块”实际上是一个新的集成变量,如果一切顺利,那么积分会严重简化。
它总是有用吗？不可以,或者说不同,您可以始终替换,但它不会总是将其转换为更容易的积分。
为什么甚至尝试这种方法？好吧,因为它经常工作。它通常是您应该尝试的第一个技巧,如果您需要解决不琐碎的那个。
如果您需要应用此方法,让我们介绍几个步骤：
第1步：
检查您正在集成的功能并查找“块”,这是\(x\)的函数,它在您正在集成的功能中显示一个或多次。
第2步：
您正在寻找的“块”需要具有非常特定的属性：块的导数需要在集成的函数中显示一次,并且只有一次。
第3步：
如果上一步是成功的,则可以使用“块”作为新变量,您可以将变量和差异替换为新变量,并且您正在解决的积分变得更加简单。
技术说明 ：通常我试图保持所有解释,并尽量避免技术。在这种情况下,我必须给出替代方法的技术解释,不要将事情过于非正式的“块”。
如果您不喜欢技术性,您可以跳到下一节,在那里您将看到这些示例。
因此,整个想法是集成给定的函数\(f(x)\)。所以我们需要找到：
\[\int f(x) \, dx\]说函数\(f(x)\)不仅仅是任何功能,它都有一定的特定结构,具体而具体
\[f(x) = g(h(x))h'(x)\]并且假设存在函数\(G(x)\),因此\(G'(x) = g(x)\)（所以然后\(G\)是\(g\)的反导体）。然后,我们得到了
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]这是为什么？？？ 嗯,简单：根据定义,反导体是一个函数,以便当您区分它时,您可以获得您正在集成的功能。
在这种情况下,如果您有区分\( G(h(x)) \)您得到
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]通过链条规则.....和Shazam！你拥有了它。告诉你这并不难。
替代方法的例子
关于学习如何整合的最好方法是练习。有些人会高兴地看着证明,但大多数人都希望在实践中看到事情。
所以,让我们进入实际的理由。
例1
找到以下无限制的积分：
\[\int x \sin(x^2)\,dx\]回答：
根据第1步,我们正在寻找一个块,一个非常特定的块。如果您查看积分,则集成变量是\(x\)。
使用此技术时,可能会有很多试验和错误。说我们考虑以下块：
\[u = x^2\]我们知道这个块很好,因为它的衍生品是\(u' = 2x\),它出现在积分中。
但是你说“我看到了\(x\),但我看不到2”。好吧,没有必要上衣。我们可以做伎俩。遵守这一点
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]你是谁,Mandrake魔术师???一边笑话,那个小技巧有效。因此,块替换是
\[u = x^2\] \[du = 2x \, dx\]（\(du = 2x \, dx\)的符号是允许的,技术上不正确,但它具有坚实的基础,所以忍受它）。因此使这笔替换变成了整体
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]因此,一旦更改为新变量\(u\),积分变为更易于解决\(\sin(u)\)的积分。一旦你解决了它,你必须记得回到原来的变量。
例2.
现在,让我们进入一个稍微复杂的例子。计算无限的积分
\[\int e^{x+e^x} \,dx\]使用U-替代方法。
回答：
你说的是什么???好吧,这并不难。请注意,无限积分可以重新编写为：
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]所以,现在你看到你集成的功能的新形式,你能想出一个“块”或“U-替代”??
请记住,不要害羞地进行试用和错误。如果某些东西不起作用,请尝试别的东西。如果你试过\(u = e^x\)怎么办？
块的导数是\(u' = e^x\),它在原始功能中找到一次。而且：
\[u = e^x\] \[du = e^x \, dx\]所以我们得到：
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]更多关于替代的整合
让我们面对：集成可能很难。真的很难。一些不太复杂的函数（至少由外表）给了数学家一个非常困难的时间来处理。
一些其他不太复杂的函数（至少通过所述外观）根本无法通过基本方法来解决。
所以,你最好相信整合可能是一个艰难的磨难。所以你必须做好准备。
最简单的工具和非常常用的技术是通过替换的集成技术。是的,它被使用,因为它常常在测试或作业中常见。
但我们欺骗了一点点。实际上,具有替代技术求解的正确结构的积分非常具体。您看到许多例子的原因是因为它们是非常具体的函数,这些功能是为了与该技术集成的。
但允许我钝：如果您的软件程序旨在生成随机函数,并且它确实为您生成一个,您将能够使用替换技术的机会是瘦的。
尽管如此,它是一种强大的小集成技术,适用于一类非常具体的积分。
什么是U替代技术？
具有无限积分的𝘶替换只是替代方法的另一个名称。它被称为“𝘶替换”,因为使用的块名为\(u\),因此新变量将是u。
这绝对不是一个好名字,因为您选择的块的名称完全无关紧要计算积分的过程。您可以调用块（和新变量）\(z\),它不会产生差异。