Substitution Method of Integration
The Substitution Method of Integration or Integration by Substitution method is a clever and intuitive technique used to solve integrals, and it plays a crucial role in the duty of solving integrals, along with the integration by parts and partial fractions decomposition method.
Integration can be a difficult operation at times, and we only have a few tools available to proceed with it.
Naturally, the calculation of the indefinite integral for some basic elementary functions (such as polynomials, powers, elementary trigonometric functions, etc) is very simple.
But the question is how to proceed with computing the indefinite integral (or primitive) for more complex functions or for the algebraic combination of functions.
Are you ready to rock?? I am, so follow me.
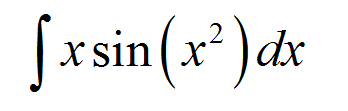
How Does the Substitution Method Work?
The method of integration by substitution works by identifying a "block" that contains the integration variable, so that the derivative of that block can also be found inside of the integral. This method is also commonly called the u-substitution method.
If the structure of the integral allows, this "block" becomes actually a new integration variable, if everything goes well, and the integral becomes seriously simplified.
![]() Does it always work? No. Or said differently, you can always do a substitution, but it won't always convert it into an easier integral.
Does it always work? No. Or said differently, you can always do a substitution, but it won't always convert it into an easier integral.
![]() Why even try this method? Well, because it works often. And it is typically the first trick you should try if you need to solve an integral that is not trivial.
Why even try this method? Well, because it works often. And it is typically the first trick you should try if you need to solve an integral that is not trivial.
Let us put out a couple of steps to follow if you need to apply this method:
![]() STEP 1:
Examine the function you are integrating and look for a "block", this is, a function of \(x\) that appears one or more times in the function you are integrating.
STEP 1:
Examine the function you are integrating and look for a "block", this is, a function of \(x\) that appears one or more times in the function you are integrating.
![]() STEP 2:
The "block" you are looking for needs to have a very specific property: the derivative of the block needs to appear one time and one time only in the function that is being integrated.
STEP 2:
The "block" you are looking for needs to have a very specific property: the derivative of the block needs to appear one time and one time only in the function that is being integrated.
![]() STEP 3:
If the previous steps were successful, you can use the "block" as the new variable, and you can replace the variable and the differential to the new variable, and the integral you are solving now becomes much simpler.
STEP 3:
If the previous steps were successful, you can use the "block" as the new variable, and you can replace the variable and the differential to the new variable, and the integral you are solving now becomes much simpler.
Technical Note : Usually I try to keep all explanations simple, and try to avoid technicalities. In this case, I will have to give the technical explanation for the substitution method, to not to leave things too informal with the idea of the "block".
If you do not like technicalities, you can skip to the next section, where you will see the examples.
So, the whole idea is to integrate a given function \(f(x)\). So we need to find:
\[\int f(x) \, dx\]Say that the function \(f(x)\) is not just any function, and it has a certain specific structure, specifically
\[f(x) = g(h(x))h'(x)\]and assume that there is a function \(G(x)\) so that \(G'(x) = g(x)\) (so then \(G\) is the antiderivative of \(g\)). Then, we get that
\[\int f(x) \, dx = \int g(h(x))h'(x) \, dx = G(h(x)) + C\]Why is that??? Well, simple: By definition, an antiderivative is a function so that when you differentiate it, you get the function you are integrating.
In this case, if you differentiate \( G(h(x)) \) you get
\[\displaystyle \frac{dG(h(x)}{dx} = G\,'(h(x))h'(x) = g(h(x))h'(x)\]by the Chain Rule.....and shazam! you have it. Told you it was not that hard.
Examples of the Substitution Methods
The best way to go about learning how to integrate is to practice. Some people will rejoice from looking at proofs, but majority of people will want to see things in practice.
So, let us move into practical grounds.
EXAMPLE 1
Find the following indefinite integral:
\[\int x \sin(x^2)\,dx\]ANSWER:
According to Step 1, we are looking for a block, a very specific block. If you look at the integral, the integration variable is \(x\).
There is a lot of trial and error, potentially, when using this technique. Say that we consider the following block:
\[u = x^2\]We know that this block is good because the derivative of it is \(u' = 2x\), which appears in the integral.
But then you say "I see the \(x\) but I don't see the 2". Well, there is no need to be uptight. We can do a trick. Observe that
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx\]Who are you, Mandrake the Magician??? Jokes aside, that little trick works. So, the block substitution is
\[u = x^2\] \[du = 2x \, dx\](the notation of \(du = 2x \, dx\) is permissive and technically incorrect, but it has solid foundation, so bear with it). So making this substitution transform the integral to
\[\displaystyle \int x \sin(x^2)\,dx = \frac{1}{2}\int 2x \sin(x^2)\,dx \] \[\displaystyle = \frac{1}{2}\int \sin(u)\,du \] \[\displaystyle = -\frac{1}{2} \cos(u) + C \] \[\displaystyle = -\frac{1}{2} \cos(x^2) + C \]So, once you changed to the new variable \(u\), the integral became into an easier to solve integral of \(\sin(u)\). Once you solved it, you MUST remember to come back to the original variable.
EXAMPLE 2
Now, let us move into a slightly more complicated example. Compute the indefinite integral
\[\int e^{x+e^x} \,dx\]using the u-substitution method.
ANSWER:
What is this you say??? Well, it is not that hard. Notice that the indefinite integral can be re-written as:
\[\int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \]So, now that you see the new form of the function you are integrating, can you come up with a "block" or "u-substitution"??
Remember, don't be shy of doing trial and error. If something does not work, try something else. What if you tried \(u = e^x\)?
The derivative of the block is \(u' = e^x\), which is found once in the original function. Moreover:
\[u = e^x\] \[du = e^x \, dx\]So we get:
\[\large \int e^{x+e^x} \,dx = \int e^x e^{e^x} \,dx \] \[\large = \int e^{e^x} e^x \,dx \] \[\large = \int e^{u} \,du \] \[\large = e^{u} + C\] \[\large = e^{e^x} + C\]More About Integration by Substitution
Let's face it: Integration can be hard. Really hard. Some not-too-complicated functions (at least by the looks) have given mathematicians a terribly hard time to deal with.
Some other not-too-complicated functions (at least by the looks again) are simply not solvable by elementary methods.
So, you better believe that integration can be a tough ordeal. So you have to go prepared.
One of the easiest tools, and very commonly used technique is the technique of integration by substitution. Yes, it is used because it appears frequently on tests or homework.
But we cheated a little bit. In reality, integrals that have the right structure to be solved by the substitution technique are very specific. The reason you see lots of examples of that is because they are very specific functions that are meant to work to be integrated with that technique.
But allow me to be blunt: If you have a software program that is designed to generate random functions, and it does generate one for you, chances that you will be able to use the substitution technique are slim.
Still, it is a powerful little integration technique that works for a very specific class of integrals.
What is the u-substitution technique?
The 𝘶-substitution with indefinite integrals is just another name for the substitution method. It is called "𝘶-substitution" because the block that is used is named \(u\), so the new variable will be u.
This is definitely not a good name, because the name you choose for your block is completely irrelevant for the process of computing the integral. You can call the block (and your new variable) \(z\) and it would not make difference.
