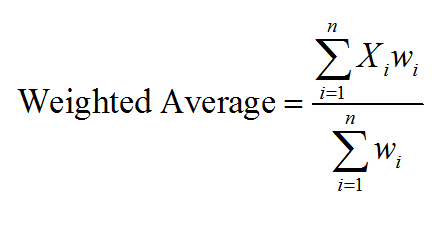(See Solution) Using Fourier integral transforms, find the displacement u(x, t) 4 (partial^2 u)/(∂ x^2)=(partial^2 u)/(partial t^2), u(0, t)=0, t>0 u(x,

Question: Using Fourier integral transforms, find the displacement

\[u(x, t)\] \[4 \frac{\partial^{2} u}{\partial x^{2}}=\frac{\partial^{2} u}{\partial t^{2}}, \quad u(0, t)=0, \quad t>0\]

$u(x, 0)=x e^{-x}, x>0$, and $\left.\frac{\partial u}{\partial t}\right]_{t=0}= \begin{cases}x, 01\end{cases}$

Price: $2.99

Solution: The downloadable solution consists of 2 pages
Deliverable: Word Document

∴ Other downloads you may be interested in ∴

$(Solution Library) Find the solution φ of y^prime \prime+(x-1)^2$ (Solution Library) Find the solution φ of y^prime \prime+(x-1)^2

(Solution Library) s (a.) through (e.) indicate how properties

[Solved] Find the first 7 nonzero terms of the Maclaurin series

$[See Steps] Show that W[J_nu, J_-\nu](x)=C/x for$ [See Steps] Show that W[J_nu, J_-\nu](x)=C/x for any positive number

(Solution Library) Use the given change of variables to transform

Use this Weighted Average Calculator - MathCracker.com

(See Solution) Using Fourier integral transforms, find the displacement u(x, t) 4 (partial^2 u)/(∂ x^2)=(partial^2 u)/(partial t^2), u(0, t)=0, t>0 u(x,

reset password

sign up