Абсолютное неравенство
Неравенство абсолютных ценностей - это неравенство, в котором есть одно или несколько абсолютная величина . Напомним, неравенство почти похоже на уравнение, но вместо знака "=" стоит "≤" или "≥".
Это различие приводит к тому, что набор решений обычно представляет собой область, как и для большинства неравенств. И тот факт, что речь идет об абсолютных величинах, указывает на особый подход к их разрешению.
В этом руководстве мы сконцентрируемся на конкретных навыках, необходимых для разрешения этого типа неравенства, содержащего одно или несколько абсолютных значений. Также предположим, что в неравенстве участвуют одна или две переменные, \(x\) и / или \(y\).
Что такое абсолютное неравенство?
Для целей этого анализа мы будем рассматривать неравенство по абсолютной величине как неравенство, включающее одну или две переменные, по крайней мере, с одним абсолютным значением.
Например, ниже у нас есть неравенство абсолютных значений с двумя переменными \(x\) и \(y\):
\[|3x+2y-1| \ge 1\]Или, кроме того, мы могли бы иметь следующее неравенство по абсолютным значениям только с одной переменной:
\[|3x-1| \le 2\]Для наших целей и для целей методов, используемых для их разрешения, мы будем иметь дело с неравенствами обоих типов (одна и две переменные)
Как разрешить абсолютное неравенство ценностей?
При решении уравнений или неравенств на самом деле не существует серебряной пули, которая решает все. Каждая проблема индивидуальна и может иметь свои особенности.
Лучшее, что мы можем сделать, - это предложить серию шагов, которые помогут вам в процессе разрешения неравенства.
Шаг 1:
Для каждого абсолютного значения определите области, в которых аргумент абсолютного значения отрицательный, а где неотрицательный.
Шаг 2:
Если в неравенстве есть только одно абсолютное значение, решите его в обеих областях (где аргумент абсолютного значения отрицательный, а где он неотрицательный).
Шаг 3:
Если в неравенстве более одного абсолютного значения, необходимо пересечь все регионы, чтобы получить набор меньших разделов. В каждом разделе нужно ТОЧНО знать знак каждого аргумента. Затем решите неравенство во всех областях.
Шаг 4:
Как только вы получите частичное решение, которое находится в каждой из областей, окончательное решение будет простым объединением этих частичных решений.
Проще говоря: вам нужно выяснить области, в которых вы точно знаете знак аргумента абсолютных значений (чтобы от них можно было избавиться).
Несколько примеров должны прояснить эти шаги.
ПРИМЕР 1
Решите следующее неравенство
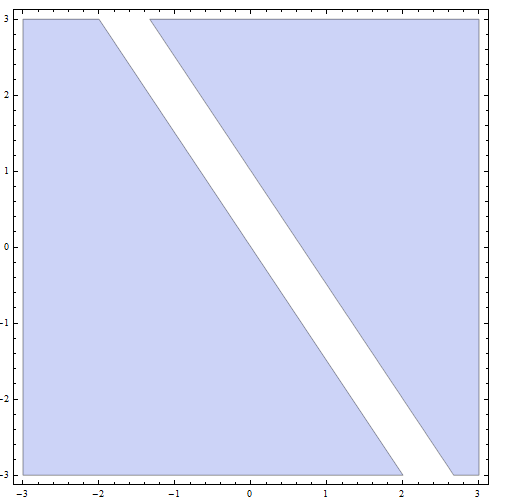
\[| 2x + 4y - 1 | \ge 2\]ОТВЕЧАТЬ:
Чтобы решить неравенство, нам нужно использовать шаги, указанные выше.
Шаг 1: Существует только одно абсолютное значение, поэтому нам нужно определить, является ли аргумент отрицательным или неотрицательным. Следовательно, нам нужно сначала решить:
\[2x + 4y - 1 \ge 0\]Есть несколько стратегий для решения вышеуказанного, но самый простой - сначала решить уравнение
\[2x + 4y - 1 = 0\]что означает, что \(4y = -2x + 1\) или то же самое, что и \(y = -\frac{1}{2}x + \frac{1}{4}\), что соответствует линии с уклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\).
Теперь, чтобы позаботиться о \(2x + 4y - 1 \ge 0\), мы проверяем, удовлетворяет ли точка \((0,0)\) неравенству:
\[2(0) + 4(0) - 1 = -1 < 0\]Итак, \((0,0)\) удовлетворяет или не удовлетворяет неравенству. Напрашивается вывод, что линия с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\) делит плоскость на две области:
Для точек ниже линии (мы называем эту область 1, \(R_1\)) мы получаем, что \(2x + 4y - 1 < 0\)
Для точек над линией, включая саму линию (мы называем эту область 2, \(R_2\)), мы получаем, что \(2x + 4y - 1 \ge 0\)
Почему это важно? Почему мы берем на себя все эти проблемы? Потому что на \(R_1\) мы получаем это с \( 2x + 4y - 1 < 0\), затем \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). Точно так же на \(R_2\) мы получаем это, поскольку \( 2x + 4y - 1 \ge 0\), затем \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
Шаг 2: Теперь нам нужно решить неравенство на участке 1, \(R_1\) :
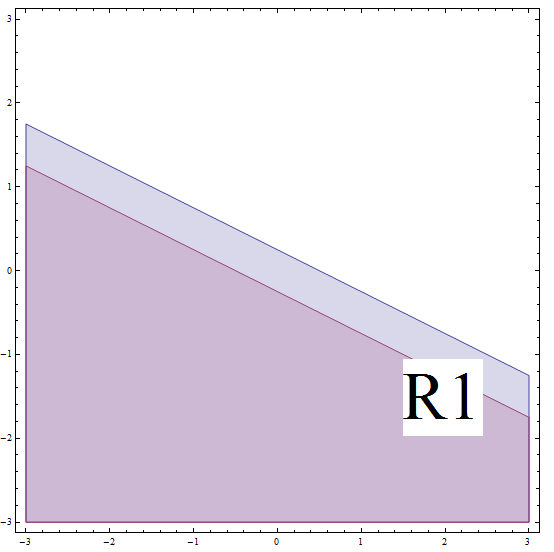
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]Это соответствует всем точкам ниже или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\). Но не забывайте, что вы находитесь на \(R_1\), и эта линия, которую мы обнаружили, находится НИЖЕ границы \(R_1\) (см. График ниже).
Чтобы уточнить, поскольку мы находимся в предположении, что мы находимся в \(R_1\), нам нужно, чтобы мы были НИЖЕ линией с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{1}{4}\). Исходя из этого предположения, мы решили исходное неравенство, и нам также необходимо находиться ниже линии с наклоном \(m = -\frac{1}{2}\) и точкой пересечения по оси Y \(n = -\frac{1}{4}\). Эти два условия должны выполняться одновременно, поэтому мы получаем пересечение двух областей.
Итак, частичное решение в этом случае соответствует всем точкам ниже или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\).
Теперь нам нужно решить неравенство в области 2, \(R_2\) :
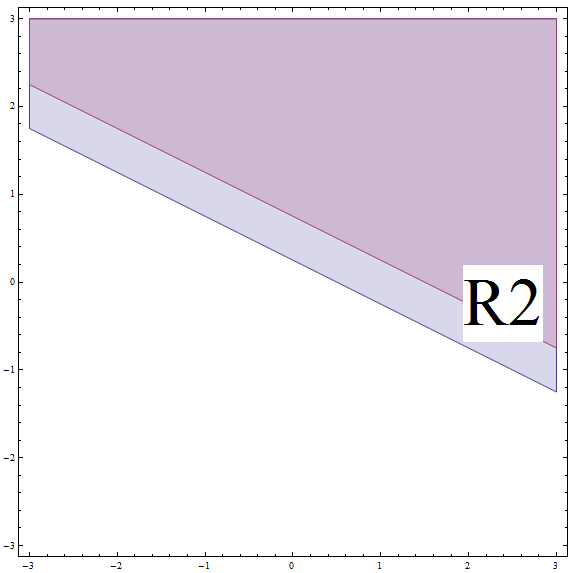
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]Это соответствует всем точкам выше или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{3}{4}\). Но не забывайте, что вы находитесь на \(R_2\), и эта линия находится НАД границей \(R_2\) (см. График ниже).
Находя пересечение между \(R_2\) и областью выше, мы получаем, что решение части в этом случае - это все точки выше или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = \frac{3}{4}\).
Шаг 4: Теперь окончательное решение - это объединение всех решений частей из предыдущих частей: окончательное решение - это все точки НИЖЕ или на линии с наклоном \(m = -\frac{1}{2}\) и пересечением по оси Y \(n = -\frac{1}{4}\), ПЛЮС все точки НАДЕЖДА или на линии с наклоном \(m = -\frac{1}{2}\) и Y-перехват \(n = \frac{3}{4}\).
Графически получаем
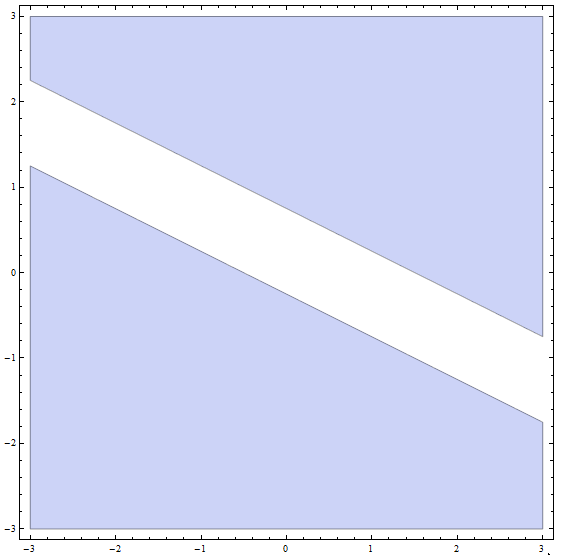
что завершает разрешение неравенства.
ПРИМЕР 2
Решите следующее двойное неравенство абсолютных значений
\[| 2x - 1 | \ge |x + 3|\]ОТВЕЧАТЬ:
Это двойное неравенство по абсолютным значениям, потому что существует 2 абсолютных значения. Это означает, что поиск регионов потребует немного больше работы (условно говоря).
Шаг 1: Для первого абсолютного значения мы решаем:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]Итак, мы получаем \(2x- 1 \ge 0\) на \([\frac{1}{2}, +\infty)\) и \(2x- 1 < 0\) на \((-\infty, \frac{1}{2})\).
Для второго абсолютного значения решаем:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]Итак, мы получаем \(x+3 \ge 0\) на \([-3, +\infty)\) и \(x+3 < 0\) на \((-\infty, -3)\).
Итак, мы определяем 4 региона:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). В этом регионе мы получаем: \(2x- 1 \ge 0\) AND \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). В этой области мы получаем: \(2x- 1 \ge 0\) AND \(x+3 < 0\), хотя эта область пуста.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). На этом участке получаем: \(2x- 1 < 0\) AND \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). В этом регионе мы получаем: \(2x- 1 < 0\) AND \(x+3 < 0\).
Шаг 2: Теперь нам нужно решить двойное неравенство по абсолютным значениям для каждой из четырех областей:
• \(R_1\):
Здесь мы получаем \(2x- 1 \ge 0\) AND \(x+3 \ge 0\), так что тогда
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]Итак, чтобы получить частичное решение, нам нужно пересечь \(x \ge 4\) или \([4, +\infty)\) с \(R_1\).
Следовательно, соответствующее решение детали: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• \(R_2\):
Эта часть решения пуста (\(\varnothing\)).
• \(R_3\):
Здесь мы получаем \(2x- 1 < 0\) AND \(x+3 \ge 0\), так что тогда
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]Итак, чтобы получить это частичное решение, нам нужно пересечь \( x \le -\frac{2}{3}\) или \( (-\infty, -\frac{2}{3}]\) с \(R_3\).
Следовательно, соответствующее решение детали: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• \(R_4\):
Здесь мы получаем \(2x- 1 < 0\) AND \(x+3 < 0\), так что тогда
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]Итак, чтобы получить это частичное решение, нам нужно пересечь \( x \le 4 \) или \((-\infty, 4]\) с \(R_4\).
Следовательно, соответствующее решение детали: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
Шаг 4:
Наконец, мы получаем объединение частичных решений, чтобы получить, что решение начального данного неравенства
Никто не сказал, что это будет коротко, правда? Хорошо. Это не очень сложно, просто нужно действовать систематически и придерживаться плана.
Подробнее о неравенствах с абсолютным значением
Почему мы вообще беспокоимся о подобном неравенстве? Нам это не безразлично, потому что у них действительно есть приложения на практике.
Например, в геометрии расстояния на реальной прямой должны быть представлены как абсолютные значения, поскольку они должны быть неотрицательными.
Может возникнуть определенная геометрическая ситуация, в которой вам нужно найти все точки на реальной прямой, которые находятся на расстоянии как минимум 2 от точки 3. Такая ситуация может быть описана следующим неравенством:
\[| x-3 |\ge 2\]Давайте разберемся в указанном выше неравенстве. Точка \(x\) - это точка, в которой мы хотим удовлетворить неравенство. Расстояние от \(x\) до точки 3 обозначается как \(|x - 3|\).
Затем мы пытаемся найти точки, которые находятся на расстоянии не менее 2 от точки 3, поэтому расстояние \(|x - 3|\) должно быть не менее 2, что объясняет \(|x - 3| \ge 2.\)
Это всего лишь один из видов проблем неравенства абсолютных ценностей, с которыми вы можете столкнуться на практике.
Можете ли вы найти абсолютные неравенства без решения?
Вы делаете ставку. Вот вам один \(|2x| < |x|\). Неравенство может оказаться просто невыполнимым, как в случае с тем, которое я вам только что привел.
Как насчет графического отображения неравенства абсолютных значений?
Процесс их построения графиков по существу идет рука об руку с процессом их решения: вам нужно найти области, в которых вы точно знаете, являются ли аргументы абсолютных значений положительными или отрицательными, а затем неравенства абсолютных значений превращаются в простые неравенства, что тривиально изображено на графике. Затем все кусочки полученных областей просто соединяются.