Алгебра Учебники

Биномиальная теорема

Биномиальная теорема - одна из наиболее известных теорем алгебры, которая имеет множество приложений в области алгебры, теории вероятностей и статистики. В нем изложена красивая и краткая формула для n ^th степень суммы двух значений: \((a+b)^n\)

Впервые меня неофициально представил сэр Исаак Ньютон в 1665 году.

Многие другие известные математики взялись за биномиальную теорему после Ньютона. Это была очень интересная проблема в 17-18 веках.

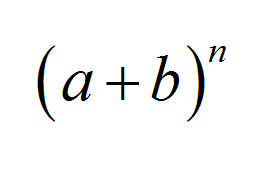
Формула биномиального разложения

Целочисленность биномиальной теоремы заключается в том, что она дает очень элегантную и лаконичную формулу. Прежде чем перейти к формуле, давайте сделаем некоторые вычисления. Например, для \(n = 2\) получаем:

\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]

Теперь попробуем с \(n = 3\):

\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]

Наконец, давайте проявим смелость и попробуем с \(n = 4\):

\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]

Хорошо, это было храбро, да? Вы видите там какие-то закономерности. Я кое-что вижу. Например, для \(n = 2\) мы могли бы упростить его до 3-х членов. Для \(n = 3\) мы могли бы упростить его до 4 терминов, а для \(n = 4\) мы могли бы упростить его до 5 терминов. В общем, я ожидаю, что для общей мощности \(n\) у нас будут условия \(n+1\).

Еще шаблоны? Что ж, всегда есть член формы \(a^l b^m\), и мы можем видеть, что полномочия \(l\) уменьшаются, а полномочия \(m\) возрастают. Но есть кое-что интересное: если вы проверите каждый член, сумма степеней всегда будет \(n\). Действительно, вы проверите, что \(l + m = n\) для всех этих условий.

Например, для \(n = 2\) у вас есть термин \(2 a b\). Степень \(a\) равна 1, мощность \(b\) равна 1, а сумма степеней равна \(1 + 1 = 2\). Или, например, для \(n = 4\) у вас есть член \(6 a^2 b^2\), где степень \(a\) равна 2, а степень \(b\) равна 2, а сумма степеней равна \(2 + 2 = 4\)

Общая биномиальная теорема

Теперь мы готовы дать общее выражение биномиальной теоремы. Готовый? У нас есть:

\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]

где термин \({n \choose i}\) читается как "n выбирают i" или также как "комбинаторный коэффициент", и определяется как

\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]

Например,

\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]

Вы можете использовать это калькулятор комбинаторных коэффициентов чтобы узнать больше об этом и попрактиковаться, просмотрев все показанные шаги.

Общая биномиальная теорема с использованием суммирования

В приведенной выше сумме, определяющей биномиальную теорему, используются обозначения по расширению, чтобы сделать термины более понятными. Как всегда в математике, мы стараемся сделать вещи более компактными, и приведенное выше выражение можно резюмировать как:

\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]

Обратите внимание на силу терминов в расширении. Общий термин - \(a^i b^{n-i}\) (умноженное на константу). Сумма полномочий \(i + (n-i) = n\). Таким образом, сумма степеней ВСЕХ терминов в раскрытии должна быть \(n\). Разве это не красиво ???

ПРИМЕР 1

Может ли термин \(x^3 y^2\) (умноженный на константу) быть частью расширения \((x+y)^6\)? Почему?

ОТВЕЧАТЬ:

Ответ - нет. В этом случае \(n = 6\), и мы знаем из биномиальной теоремы, что сумма степеней членов \(x^l y^m\) в разложении должна быть равна \(n\). В этом случае \(l + m = 3 + 2 = 5\), что не то же самое, что \(n = 6\). Следовательно, термин \(x^3 y^2\) (умноженный на константу) не может быть частью расширения \((x+y)^6\).

ПРИМЕР 2

Разверните \((a-b)^3\), используя биномиальную теорему.

ОТВЕЧАТЬ:

Ждать. Вы, должно быть, думаете: "Ты только что научил меня расширять \((a+b)^n\), но теперь ты спрашиваешь меня о \((a-b)^n\). Почему ты такой жестокий". Подожди. Я не обманываю тебя.

Всегда есть уловка (не забудьте эту строку, она часто встречается в математике).

Обратите внимание, что \(a - b\) совпадает с \(a + (-b)\).

Ааааааааааааааааааааааааааааааааа, так что биномиальная теорема все еще применима. Итак:

\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]

Подробнее о биномиальном разложении

Биномиальная теорема настолько важна, что изучается практически во всех курсах, включая алгебру, исчисление, вероятность и статистику.

Есть некоторые обобщения, такие как отрицательное биномиальное расширение, которое выходит за рамки этого руководства.

Треугольник Паскаля

Иногда студенты застревают, когда им нужно вычислить константы (комбинаторные коэффициенты), входящие в биномиальное разложение. Один из действительно простых способов сделать это - использовать треугольник Паскаля.

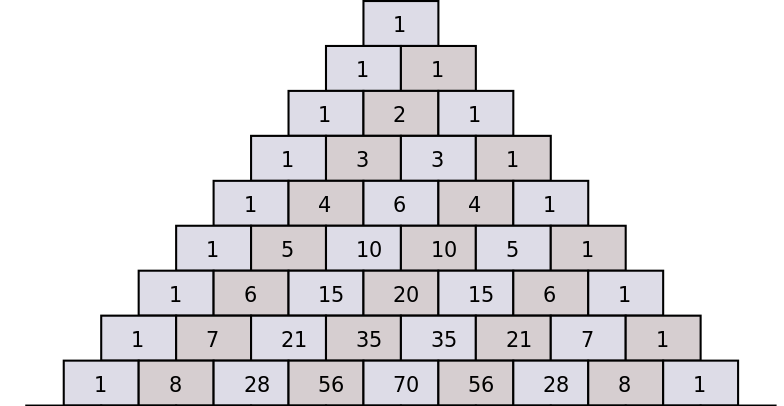
Треугольник Паскаля показывает, как последовательные биномиальные коэффициенты могут быть вычислены на основе коэффициентов предыдущего значения \(n\), путем сложения двух коэффициентов, которые идут непосредственно выше.

Приложения

Биномиальное расширение имеет множество приложений в алгебре и теории вероятностей. Например, в "Вероятности" биномиальное распределение основано на биномиальной теореме.

Действительно, рассмотрим число \(0 \le p \le 1\). Затем \(p + (1-p) = 1\), и мы можем использовать биномиальную теорему:

\[\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} \]

что обозначает

\[\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1 \]

Оказывается, каждый из членов \({n \choose i} p^i (1-p)^{n-i}\) представляет собой вероятность. Кроме того, у нас есть:

\[\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1 \]

где \(X\) - количество успехов после \(n\) испытаний, когда вероятность успеха каждого испытания равна \(p\). Переменная \(X\) известна как биномиальная случайная величина.