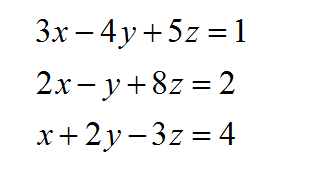There are 10 variables and 84 observations in the file. Your task is to develop a regression equation for predicting the probability of capture for small mammals (Variable 10) from any of the variables 1-9 or simple transformations thereof. You can consider powers, logs, antilogs (exponential functions), trig functions, or roots. Use all you know to test the adequacy of the model. The objective is to produce the best model possible. When you have chosen the model you feel is best, find the 90% confidence and prediction intervals for x = a vector with X ₀ =1, X ₁ =87, X ₂ =4, X ₃ =15, X ₄ =12, X ₅ =2, X ₆ =0.6, X ₇ =1, X ₈ =17, X ₉ =0.3 (You only need to use values for the variables that are included in your final model). The X'X inverse is available by specifying the option I in the model statement of SAS PROC REG or by saving it as an option in MINITAB. The variables are

1. Year
2. Month
3. Maximum temperature during the trapping period (C)
4. Minimum temperature during trapping (C)
5. Precipitation in the month preceding trapping (cm)
6. Cloud cover during trapping (proportion of sky covered)
7. Precipitation during trapping (cm)
8. Wind velocity during trapping (mph)
9. Lunar phase (moon as proportion of full)
10. Probability of capture

Do not simply turn in annotated computer output. Relevant information may be included in tables or figures (which may be excerpts from output), but the important results and conclusions must be covered in the body of your paper. Your discussion and conclusions should include a brief discussion of the form of general relationships between predictors and dependent variable, but do not try to explain biological mechanisms underlying the relationships.

Price: $18.46

Solution: The downloadable solution consists of 12 pages, 646 words and 12 charts.
Deliverable: Word Document