The manager of a vacation resort has claimed that, on average, a guest spends at least $3200 at the resort
-
The manager of a vacation resort has claimed that, on average, a guest spends at least $3200 at the resort during a one week stay, including meals and entertainment. A member of the accounting staff does not believe the amount is that high. They authorize you to settle their dispute. You take a SRS (n = 25) of guests that had stayed at the resort over the last several weeks. Tracking the spending of these guests at the resort you determine that the guests spent a mean of $3128 with a standard deviation of $110. Test the accountant's claim that the mean is actually less than $3200 versus the manager's claim that the guests spend a mean of $3200 or more (Show all work as well as appropriate distribution diagrams to receive credit. You may assume = .05 and that he population is symmetric and mounded.)
- (2) H 0 : H 1 :
- (2) What is the critical value of the test statistic? __________
- (2) State the decision rule:
- (2) Sketch the distribution showing the region(s) of acceptance and rejection in the graph.
- (3) Show computation and then state the statistical decision.
- (3) What would you tell the manager and accountant about their dispute?
-
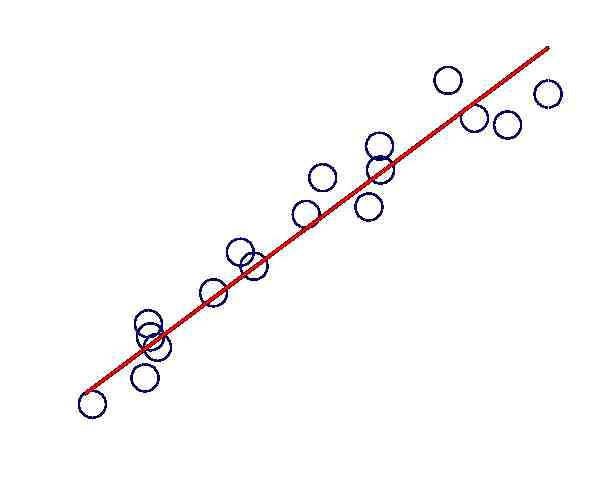
As more US houses receive cable television, the advertising revenue has continued to increase. The following data in the table show the 2004 and 2005 advertising expenditures for 10 cable television advertisers. Use your calculator to compute the regression line and the correlation coefficient.
Advertising 2004 2005 Company Expenditure Expenditure Expenditures ($1,000,000) 1 32.4 40.5 2 25.8 37.2 3 25.4 22.5 4 24.9 28.8 5 25.2 31.8 6 16.5 28.6 7 14.3 17.6 8 12.2 14.2 9 12.1 11.5 10 10.5 13.8 -
(2) In the grid above draw the scatter for this problem.
- (2) Determine the correlation coefficient. How would you describe the correlation between the 2004 Expenditures and the 2005 Expenditures? (e.g. weak—moderate—strong; positive—negative) Explain your answer.
-
(3) Determine the regression equation:
-
(2) Use the regression equation to predict the 2005 expenditure for a company that spent $23.5 million in 2004? (Show your work.)
- (2) Draw the regression line on the graph.
-
(2) Why can't you predict expenditures for a company that spent 39.2 million in 2004?
- (2)Were the 2005 Expenditures for Company # 3 more or less than expected? Explain.
-
(2) In the grid above draw the scatter for this problem.
-
(8 - 2 ea) A business woman is gathering information on a sample of small businesses in the Central Ohio region. . She visits the small business bureau and obtains a list of the businesses arranged by city. She uses a random number table to choose numbers between 0 and 800 and then selects those 35 businesses. What type of sampling did she use?
_________
A business woman is gathering information on a sample of small businesses in the Central Ohio region. . She visits the small business bureau and obtains a list of the businesses arranged by city. She selects a random number between one and 8 and gets 4. She selects the fourth business and every 7 th business after that. What type of sampling did she use?
_____________
A business woman is gathering information on a sample of small businesses in the Central Ohio region. She visits the small business bureau and obtains a list of the businesses arranged by city. She randomly chooses 5 businesses out of each city listed. What type of sampling did she use?
___________
A business woman is gathering information on a sample of small businesses in the Central Ohio region. . She visits the small business bureau and obtains a list of the businesses arranged by city. She randomly chooses 5 cities and selects all of the businesses in those cities. What type of sampling did she use? ____________________
-
According to
USA Today
(April 11, 1995), the mean number of days per year that business travelers are on the road for business is 115 with a standard deviation of 60 days per year. Assume that these results apply to the population of all business travelers and that the distribution of travel days is relatively normal. A sample of 25 business travelers was selected from the population. The mean of the sample was 127 days on the road with a standard deviation of 43 days per year.
-
(3) In this problem identify the following variables:
= __, = __, \[\bar{x}\] = __., s = __, and n = ______
- (3) What is the probability that a single business traveler will spend 127 or more days on the road?
-
(2) What is the value of the standard error of the mean for this problem?
- (3) What is the probability that any sample mean of 25 travelers will be equal to or more than 127 days per year?
-
(3) In this problem identify the following variables:
-
A farmer who raises sheep has over 1800 sheep. He needs to determine the mean weight of the herd of sheep before he sells them.
- (5) How many randomly selected sheep does he need to weigh to estimate, with a 95% confidence, the mean weight within 1.50 pound if prior studies indicate that the standard deviation of all weights is around 6 pounds? (Show work)
-
A human resource manager is trying to determine if the amount spent on health care by his company for employees differs from the average amount spent by similar companies. He has access to the records of all employees at this company and so he determines that the average per person expenditure by his company was $14,580. He needs to determine the mean amount spent by employees of other firms. To accomplish this he takes a random sample of 25 employees at a number of different companies similar to his and collects the amounts spent on their health care. His sample has a mean of $13,650 with a standard deviation of $1,200.
-
(2) In the problem find:
\[\bar{x}\]
= ___ s = __ n = __ = __
-
(4) Based on his sample construct a 95% confidence interval for the mean amount spent by all other companies on health care. (Show formula with values for credit.)
-
(3) Respond to his claim based on your results.
-
(2) In the problem find:
\[\bar{x}\]
= ___ s = __ n = __ = __
-
A recent survey of random drivers on a highway by the Highway Patrol revealed that 456 out of 500 drivers were properly belted into their seats.
-
(2) Construct a 95% confidence interval for the proportion of all drivers (on that section of highway) that wear their seatbelts. (Show your work or formula.)
-
(3) Explain the interval so that someone with no statistical background can understand it.
-
(2) Construct a 95% confidence interval for the proportion of all drivers (on that section of highway) that wear their seatbelts. (Show your work or formula.)
-
(5) A political pollster has been hired by the candidate to see if he will be elected. The election is known to be fairly close. What size of a sample will the pollster need to take to be 95% confident of the vote within 1 percentage point? (Show your work)
-
You have been hired by a consumer research agency to perform a study of consumer response to two different non-electric shavers. One of the shavers is designed to give a "close" shave and the other is designed for use on "sensitive" skin.. You distribute 750 shavers of each type to a test market of men and women who have agreed to try the shavers and indicate a preference. After 2 weeks you survey the test market with the following results:
Test the hypothesis at the .05 level of significance that gender makes a difference in the choice of the shavers.Close Sensitive Male 142 258 Female 158 192
-
(2) State the hypotheses being tested.
-
(2) Give the computed values of the test statistic
-
(2) State the critical value of the test statistic (
Or
give the p-value of the test.)
- (2) State and explain the decision.
-
(2) State the hypotheses being tested.
-
Quick answer questions: (26 – 2 point each)
-
If the critical value of a hypothesis test is t = -2.32 and the test statistic value is
t = -2.7 what is the decision? _________ - If the null hypothesis contains a "more than or equal to" in which tail is the test run? _______
- If the probability value of a hypothesis test is p = 0.037 and is set at 2% what is the decision? ______
- A confidence interval for the proportion of all voters who favor an issue goes from 0.487 to 0.519. Can you predict if the issue will pass? ____________
- If you reject the null hypothesis which type of error might you be making? ___________
- A 95% confidence interval for a population mean goes from 295 to 317. What was the mean of the sample? ___________
-
Only one of the following numbers can be a p-value. Which one must it be?
( -0.065, 2.2 E -5, 1.35, -1.96) _________ - A regression equation is Profit = 4.2 + 2.5(Sales) If sales are 4.7, what is the expected profit? ____________
- The correlation of the selling price of a house to the square foot is r = 0.35, of the selling price to the age is r = -0.4 and of the selling price to the condition is r = 0.24. Which of these three variables is the best predictor of selling price? _______
- A scatter diagram shows that every point lies exactly on a line that line goes down from the left to the right. What is the correlation coefficient (r-value) of the relationship? _______________
- A distribution has the following parameters: = 5, n = 3 and = 0. Give the values of the data that make up this set. ____________
- A hypothesis test has a decision of "Accept the null hypothesis." What type of error might be made on this problem? __________
- A null hypothesis is µ = 15. The decision is to "fail to reject the null." A student concludes: "the test proved that the mean of the population is 15." Is this conclusion true or false? ___________
-
If the critical value of a hypothesis test is t = -2.32 and the test statistic value is
-
(8) As the manager of a diet clinic you are investigating the number of calories in various hot dogs. You purchase several different brands of beef hot dogs and several brands of chicken hot dogs. You have the lab analyze the number of calories in each of the hot dog samples with the results below. You may assume that the two populations are independent and nearly normal. You may not assume the two populations have the same standard deviations.
- Chicken Hot Dogs: 139 132 123 114 114 116 108
-
Beef Hot Dog:
136
155
158
148
178
167
131
Test the hypothesis that the calories are the same. Show all parts of the hypothesis testing process. Points will be deducted for missing parts; however, this may be done using the calculator functions. (State which calculator menus were used.)
-
(7) To test whether the mean time needed to mix a batch of material is the same for machines produced by three manufacturers, a company manager uses the three machines to mix batches of four different compounds.
| Manufacturer A | Manufacturer B | Manufacturer C |
| 20 | 28 | 20 |
| 26 | 26 | 19 |
| 24 | 31 | 23 |
| 22 | 27 | 22 |
Use the data to test whether the population mean times for mixing a batch of material differ for the three manufacturers. Use α = 0.05 Show all parts of the hypothesis testing process. Points will be deducted for missing parts; however, this may be done using the calculator functions. (State which calculator menus were used.)
Price: $40.11
Solution: The downloadable solution consists of 13 pages, 2711 words and 3 charts.
Deliverable: Word Document
Deliverable: Word Document




![[Step-by-Step] The manager of the Danvers-Hilton Resort Hotel stated [Step-by-Step] The manager of the Danvers-Hilton Resort](/images/solutions/MC-solution-library-80510.jpg)