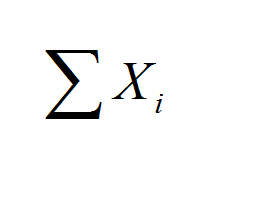1. The manager of the Danvers-Hilton Resort Hotel stated that the mean guest bill for a weekend is $ 600 or less. A member of the hotel's accounting staff noticed that the total charges for guest bills have been increasing in recent months. The accountant will use a sample of weekend guest bills to test the manager's claim.

1. Which form of the hypotheses should be used to test the manager's claim? Explain.
   
2. What conclusion is appropriate when $H_{0}$ cannot be rejected?
3. What conclusion is appropriate when $H_{0}$ can be rejected?

3. A production line operation is designed to fill cartons with laundry detergent to a mean weight of 32 ounces. A sample of cartons is periodically selected and weighed to determine whether under filling or overfilling is occurring. If the sample data lead to a conclusion of under filling or overfilling, the production line will be shut down and adjusted to obtain proper filling.

1. Formulate the null and alternative hypotheses that will help in deciding whether to shut down and adjust the production line.
2. Comment on the conclusion and the decision when \(H_{0}\) cannot be rejected.
3. Comment on the conclusion and the decision when \(H_{0}\) can be rejected

9. Consider the following hypothesis test:

\(\begin{aligned}

& {{H}_{0}}:\mu \ge 20 \\

& {{H}_{A}}:\mu <20 \\

\end{aligned}\)

A sample of 50 provided a sample mean of 19.4. The population standard deviation is 2.

1. Compute the value of the test statistic.
2. What is the \(p\) -value?
3. Using \(\alpha=.05\), what is your conclusion?
4. What is the rejection rule using the critical value? What is your conclusion?

13. Consider the following hypothesis test:

\(\begin{aligned}

& {{H}_{0}}:\mu \le 50 \\

& {{H}_{A}}:\mu >50 \\

\end{aligned}\)

A sample of 60 is used and the population standard deviation is 8 . Use the critical value approach to state your conclusion for each of the following sample results. Use $\alpha=.05$.

1. \(\bar{x}=52.5\)
2. \(\bar{x}=51\)
3. \(\bar{x}=51.8\)

17. The mean length of a work week for the population of workers was reported to be 39.2 hours (Investor's Business Daily, September 11, 2000). Suppose that we would like to take a current sample of workers to see whether the mean length of a work week has changed from the previously reported 39.2 hours.

1. State the hypotheses that will help us determine whether a change occurred in the mean length of a work week.
2. Suppose a current sample of 112 workers provided a sample mean of $38.5$ hours. Use a population standard deviation \(\sigma=4.8\) hours. What is the \(p\) -value?
3. At \(\alpha=.05\), can the null hypothesis be rejected? What is your conclusion?
4. Repeat the preceding hypothesis test using the critical value approach.

19. In 2001 , the U.S. Department of Labor reported the average hourly earnings for US production workers to be $14.32 per hour (The World Almanac 2003). A sample of wage rates for 75 production workers during 2003 is in the CD file named WageRate. Assuming the population standard deviation \(\sigma=\\) 1.45$, can we conclude that an increase occurred in the mean hourly earnings since 2001 ? Use \(\alpha=.05\).

25. Consider the following hypothesis test:

\(\begin{aligned}

& {{H}_{0}}:\mu \ge 45 \\

& {{H}_{A}}:\mu <45 \\

\end{aligned}\)

A sample of 36 is used. Identify the p-value and sate your conclusion for each of the following sample results. Use alpha = 0.01.

1. \(\bar{x}=44\) and \(s=52\)
2. \(\bar{x}=43\) and \(s=4.6\)
3. \(\bar{x}=46\) and \(s=5.0\)

27.The Employment and training Administration reported the U.S. mean unemployment insurance benefit of $238 per week. A researcher in the state of Virginia anticipated that sample data would show evidence that the mean weekly unemployment insurance benefit was below the national level.

1. Develop appropriate hypotheses that rejection of Ho will support the researcher contention.
2. For a sample of 100 individuals, the sample mean weekly unemployment insurance benefit was $231 with sample standard deviation of $80 . What in the p-value?

4. At a = .05 what is your conclusion?

d. Repeat the preceding hypotheses using he critical value approach

33. Callaway Goff Company's new forged titanium ERC driver has been described as "illegal" because it promises driving distances that exceed the USCA’s standard. Golf Digest compared actual driving distances with the ERC driver and a USGA-approved driver with a population mean driving distance of 280 yards. Based on nine test drives, the mean driving distance by the LRC driver was 286.9 yard (Got Digest, May 12,200 ) Answer the following questions assuming a sample standard deviation driving distance of 10 yards.

1. Formulate the null! and alterative hypotheses that can be used to determine whether the new ERC driver has a population mean driving distance greater than 280 yards.
2. On average how many yards farther did the golf ball travel with the ERC driver?

e. At \(a=05\), wat is your conclusion?

35. Consider the following hypothesis test:

\(\begin{aligned}

& {{H}_{0}}:p=0.20 \\

& {{H}_{A}}:p\ne 0.20 \\

\end{aligned}\)

A sample of 400 provided a sample proportion \(\bar{p}=.175\)

1. Compute the value of the test statistic,
2. What is the p -value?

1. At \(a=.05\). what is your conclusion?

d. What is the rejection rule using the critical value? What is your conclusion?

37. The Heldrich Center for Workforce Development found that 40% of internet user received more than 10 e-mail messages per day. A similar study on the use of email was repeated in 2002

1. Formulate the hypotheses that can be used to determine whether the proportion of Internet users receiving more than 10 email messages per day increased.
2. If a sample of 425 internet users found 189 receiving more than 10 email messages per day, what is the p-value?
3. At \(a = .05\). Wat is your conclusion?

41. Microsoft Outlook is the most widely used email manager. A Microsoft executive claims that Microsoft Outlook is used by at least 75% of Internet users. A sample of Internet users will be used to test this clam.

1. Formulate the hypotheses that can be used to test the claim,
2. A Merrill Lynch study reported that Microsoft Outlook is used by 72% of Internet users. Assume that the report was based on a sample size of 300 Internet users. What is the p-value?
3. At a = .05, should the executive’s claim of at least 75% be rejected?

43. An article about driving practices in Strathcona County, Alberta, Canada, claimed that 48% of drivers did not stop at stop sign intersections on county roads. Two months later, a follow up study collected data in order to see if this percentage has changed

1. Formulate the hypotheses to determine whether the proportion of drivers who did not stop at stop sign intersections had changed.
2. Assume the study found 360 of 800 drivers did not stop at stop at stop sign intersections. What is the sample proportion, what is the p-value?
3. At a = .05. What is your conclusion?

Price: $30.25

Solution: The downloadable solution consists of 11 pages, 1925 words and 1 charts.
Deliverable: Word Document