The Order of Operations
The Order of Operations is a set of conventions to conduct operations for an algebraic expression (such as \(2+3\times 4\)) when there could be an ambiguity on how to conduct the operation, because there is more than one operation.
The Order of Operations determines the precedence order of operations when evaluating an algebraic expression, which conventionally follows the PEMDAS criterion.
In the example of the algebraic expression \(2+3\times 4\), there is an addition (\(+\)) and also a multiplication (\(\times\)). Which one do I do first? Remember, operations are between two operands at a time. If I have more than two operands, I have to operate two of them first, and so on. But, which one first?
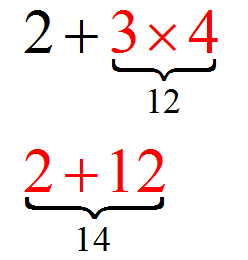
Technically, we should employ parenthesis everywhere to specific which pairs are operated first and how the operation are conducted successively.
For example, in the expression \( 2 + 3\times 4\), we could write it \( (2 + 3)\times 4\), or like \( 2 + (3\times 4)\).
So, why do we need to think about a convention for the precedence of operations when can perfectly go along with doing parentheses to avoid any ambiguity?? The answer is simplicity.
For example, what would happen with something like \( 2 + 3 \times 4 - 3/2\)?
If we are forced to specify parentheses to specify ALL the operations, we would have to write \( (2 + 3) \times (4 - 3/2)\), or \( (2 + (3 \times 4)) - (3/2)\), or \( 2 + ((3 \times 4) - (3/2))\), and on, and on, and on. It gets heavy.
So you are guessing right. As you get more operands in a more complex expression, the need to clearly specify with parenthesis all the operations to be conducted would make it really laborious to write an expression.
In general terms, making a convention for precedence of operations will save us a lot of effort in order to write unambiguous expressions.
The PEMDAS convention
The PEMDAS is mnemonic acronym that helps you remember the order of precedence of operations that is used as the standard convention to calculate algebraic expressions.
P = Parentheses first
E = Exponents next
MD = Multiplications and Divisions next
AS = Additions and Subtractions at the end
Using this convention for the order of operations, we save a lot of time by not needing to write superfluous parentheses, and only we would need them to override the default way PEMDAS does the order of calculation, if needed.
.EXAMPLE 1
Evaluate \(3+(3\times 12)\). Could you have written this expression in a simpler way?
.ANSWER:
According to PEMDAS, we conduct the operations inside the parentheses first:
\[3+(3\times 12) = 3 + 36 = 39\]This expression could have been written in a simpler way, like \(3+3\times 12\), without the parenthesis, because in that case, according to PEMDAS, you would calculate the multiplication before the sum.
EXAMPLE 2
Calculate \((18\div 6\times 5) - 14 \div 7 \).
ANSWER:
Using the PEMDAS convention, we first do the parentheses, and then do multiplications are divisions, and only I the end I do the subtraction. We get:
\[(18\div 6\times 5) - 14 \div 7 \] \[= (3 \times 5) - 14 \div 7 \] \[= 15 - 14 \div 7 \] \[= 15 - 2 \] \[= 15 - 13 \]We are doing it the long way, by showing every little step. It is ok if you do it faster, without getting so much detail, although with PEMDAS is best to go slow so to not to make any mistake.
More About the Order of Operations
Having a standard rule for the order of precedence of operations makes our life much easier when it is about writing an algebraic expression.
You need to be careful to use any necessary parentheses to express the operation you want in a correct way, because otherwise any calculator you use will have PEMDAS in place.
For the example \(2+3\times 4\), if what you want is to first multiply \(3\) and \(4\), the expression does not need parenthesis, because that is the way PEMDAS indicate to do it.
But if what you want is to first add \(2\) and \(3\), then you need to put a parenthesis like \((2+3)\times 4\), so that with PEMDAS you do the operations inside of the parenthesis first.
So, which operation should be done first?
If you paid attention to this lesson, you would have heard that the order of the operations that should be done first is determined by PEMDAS: P (Parentheses), E (Exponents), MD (multiplications and divisions) and AS (addition and subtraction).
So, why is the order of operations defined in that order?
Steps for using PEMDAS
PEMDAS is just a convention. But it is a convention that is accepted and it is convention that make sense according to other arithmetic laws.
.So PEMDAS is the standard that is used, although it is an arbitrary convention.
- Step 1: Identify the algebraic expression you want to calculate. You can conduct a quick initial consistency check to find glaring errors
- Step 2: If no glaring error are apparent, you start going through the portions of the expression as indicated by the PEMDAS rule
- Step 3: Start with portions inside parentheses, from the inner-most ones in case there are nested parentheses
- Step 4: Multiplication and division have priority, and then additions and subtractions
By the way, one funny way to remembering the PEMDAS convention is by memorizing the following very catchy phrase "please excuse my dear aunt sally ".

Is the MDAS the same as PEMDAS?
Essentially yes. MDAS stands for Multiplication - Division - Addition - Subtraction, in the sense that is the order of precedence of operations in absence of parenthesis. It is taken implicitly that parenthesis are operated first.
Does it make any difference for the order of operations with brackets
No, it does not. The bracket parenthesis fulfills exactly the same role as the regular parenthesis. If is used sometimes to break the pattern of too many nested parenthesis, just for the ease of reading.
For example, you may have something like \((((3+4)\times 4) - 3) \div 1 \). The three nested parentheses on the left side could be hard to read, so it would look easier to read if we write instead \(([(3+4)\times 4] - 3) \div 1 \). So regular and bracket parentheses are the same, but it is a good practice to alternate them in case of nested parenthesis.
Check out our algebraic expression calculator , which uses PEMDAS to operate any expression you want. Make sure you use PEMDAS, or in case of doubt about the correct precedence of operations, use parentheses.
