Normalize Data
Instructions: Using this calculator to convert data into z-scores. Enter the sample data below and the solver will provide step-by-step calculation of the normalization of the data (this is, it will calculate the corresponding z-score for each of the data values)
More About Normalizing by Converting to Z-Scores
The concept of normalizing scores, or z score normalization corresponds to computing the z-scores for all the scores provided in a dataset. This is, for each \(X_i\) score in a dataset, we compute the corresponding normalized score (z-score) following the following formula
. \[ X_i = \frac{X_i - \mu}{\sigma}\]If the population mean \(\mu\) or the population standard deviation \(\sigma\) are not known, we approximate them by computing the sample mean \(\bar X\) and the sample standard deviation \(s\).
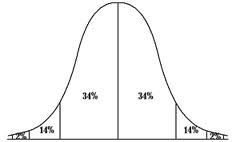
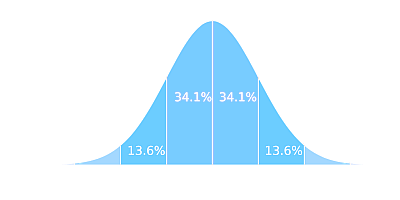
These normalized z-scores respond to a standard normal distribution , and easily calculated using standard normal tables or computational tools like Excel.
The Need for Z-scores
Why do we need normalized scores? Normalized scores present lots of advantages: First, they are dimensionless so they are great for comparing different populations. Second they tend to provide clean cut interpretation of scales, as it is typically done in Psychology, or other social sciences.
If you need compute complete descriptive statistics for your sample data, use this complete descriptive statistics calculator , or if you use this normal probability calculator to compute and graph anything related with normal probabilities, including z score probabilities.