Operations with Negative Exponents
The operations with exponents are among the most fundamental operations in Algebra, and among them, the ones that involve negative exponents are the ones that bring the most complications to students.
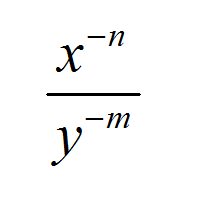
![]() First, let us recall the basic exponent properties. The use of these properties is omnipresent in most areas of Math. The rules are:
First, let us recall the basic exponent properties. The use of these properties is omnipresent in most areas of Math. The rules are:
Rule 1: \(\large \displaystyle x^0 = 1\), for \(x = \not 0\)
Rule 2: \(\large\displaystyle x^1 = x\)
Rule 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Rule 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Rule 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
For example, when you have an expression like \(3^5 \cdot 3^7\), we know we use the multiplication rule (Rule 3) to get:
\[\large 3^5 \cdot 3^7 = 3^{5+7} = 3^{12}\]The Exponent Rules: What Happens to the Negative Exponents?
Even if you did not realize it, the rules above do not say that the exponents need to be positive. Indeed, they could be negative and the rules will hold as well.
Now, from Rules 1 and 5 we can derive the relationship between positive and negative exponents. So, for Rule 5, assume that \(m = 0\) and \(n\) is positive. Then, we get
\[\large\displaystyle \frac{1}{x^n} = \frac{x^0}{x^n} = x^{0-n} = x^{-n}\]The above expression gives us a simple relationship between positive and negative exponents:
\[\large\displaystyle \boxed{\frac{1}{x^n} = x^{-n}}\]
![]() This above expression is telling us that we can pass a power with a negative exponent in the numerator to the denominator with the corresponding positive exponent. This is one 'rule' of negative exponents
This above expression is telling us that we can pass a power with a negative exponent in the numerator to the denominator with the corresponding positive exponent. This is one 'rule' of negative exponents
The beauty of the above formula is that we can cross multiply the terms on both sides of the equality, and we can write the above expression in a slightly different form:
\[\large\displaystyle \boxed{\frac{1}{x^{-n}} = x^{n}}\]
![]() This last expression is usually very useful, because it is telling us that we can bring a power with negative exponent in the denominator to the numerator but with the corresponding positive exponent. This can be considered as another "rule" for negative exponents.
This last expression is usually very useful, because it is telling us that we can bring a power with negative exponent in the denominator to the numerator but with the corresponding positive exponent. This can be considered as another "rule" for negative exponents.
EXAMPLE 1
Simplify the following expression, and leave without negative exponents:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2}\]ANSWER:
Using the rule of negative exponents, we switch positive/negative exponents between numerator/denominator:
\[\large \displaystyle \frac{x^{3}\sqrt{x} y^{-3}}{x^{-1/2} y^2} = \frac{x^{3}\sqrt{x} x^{1/2}}{ y^2 y^{3}}\] \[\large = \frac{x^{3} x^{1/2} x^{1/2}}{ y^2 y^3} = \frac{x^{3+1/2+1/2}}{ y^{2+3}} \] \[\large = \frac{x^{4}}{ y^{5}} \]and we end the simplification, because there is nothing left to simplify.
More About Negative Exponents
One of the biggest takeaways from this tutorial about negative exponents is that we have rules to turn those negative exponents into positive exponents. How do we do that?
• If we have a negative exponent in the numerator (so you are multiplying by a negative exponent), we can pass it to the denominator with positive exponent.
• If we have a negative exponent in the denominator (so you are dividing by a negative exponent), we can pass it to the numerator with positive exponent.
Operating with negative exponents is just a small part of the topic of dealing with rules of exponents , which give you a clear insight of why the case with negative exponents works the way it does.
