द्विपद प्रमेय
द्विपद प्रमेय बीजगणित में अधिक प्रसिद्ध प्रमेयों में से एक है, और इसमें बीजगणित, संभाव्यता और सांख्यिकी के क्षेत्र में बहुत से अनुप्रयोग हैं। यह n . के लिए एक अच्छा और संक्षिप्त सूत्र बताता है वां दो मानों के योग की शक्ति: \((a+b)^n\)
मुझे पहली बार अनौपचारिक रूप से सर आइजैक न्यूटन ने 1665 में प्रस्तुत किया था।
न्यूटन के बाद कई अन्य उल्लेखनीय गणितज्ञों ने द्विपद प्रमेय का अध्ययन किया है। 17वीं और 18वीं शताब्दी में यह एक बहुत ही आकर्षक समस्या थी।
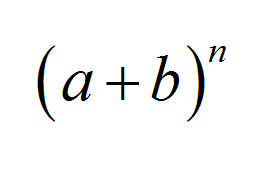
द्विपद विस्तार का सूत्र
द्विपद प्रमेय के बारे में पूर्णांक यह है कि यह एक बहुत ही सुंदर और संक्षिप्त सूत्र प्रदान करता है। सूत्र में आने से पहले, आइए कुछ गणनाएँ करें। उदाहरण के लिए, \(n = 2\) के लिए हम पाते हैं:
\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]आइए अब \(n = 3\) के साथ प्रयास करें:
\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]अंत में, आइए हम बहादुर बनें और इसे \(n = 4\) के साथ आजमाएं:
\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]ठीक है, वह बहादुर था, है ना ?? क्या आपको वहां कोई पैटर्न दिखाई देता है। मैं कुछ देख सकता हूँ। उदाहरण के लिए, \(n = 2\) के लिए हम इसे 3 पदों तक सरल बना सकते हैं। \(n = 3\) के लिए हम इसे 4 पदों तक सरल कर सकते हैं, और \(n = 4\) के लिए हम इसे 5 पदों तक सरल बना सकते हैं। तो सामान्य तौर पर, मैं उम्मीद करता हूं कि \(n\) की सामान्य शक्ति के लिए, हमारे पास \(n+1\) शब्द होंगे
अधिक पैटर्न? खैर, हमेशा \(a^l b^m\) रूप का एक पद होता है, और हम देख सकते हैं कि \(l\) शक्तियां घटती जाती हैं, और \(m\) शक्तियां बढ़ती जाती हैं। लेकिन कुछ दिलचस्प भी है: यदि आप प्रत्येक पद की जांच करते हैं, तो शक्तियों का योग हमेशा \(n\) होता है। दरअसल, आप उन सभी शर्तों के लिए उस \(l + m = n\) की जांच करेंगे।
उदाहरण के लिए, \(n = 2\) के लिए आपके पास \(2 a b\) पद है। \(a\) की शक्ति 1 है, और \(b\) की शक्ति 1 है, और शक्तियों का योग \(1 + 1 = 2\) है। या उदाहरण के लिए, \(n = 4\) के लिए आपके पास \(6 a^2 b^2\) शब्द है, जहां \(a\) की शक्ति 2 है, और \(b\) की शक्ति 2 है, और शक्तियों का योग \(2 + 2 = 4\) है।
सामान्य द्विपद प्रमेय
अब हम द्विपद प्रमेय के लिए सामान्य व्यंजक देने के लिए तैयार हैं। तैयार? हमारे पास है:
\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]जहां \({n \choose i}\) शब्द "n select i" या "कॉम्बिनेटरियल गुणांक" के रूप में पढ़ा जाता है, और इसे इस प्रकार परिभाषित किया जाता है
\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]उदाहरण के लिए,
\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]आप इसका इस्तेमाल कर सकते हैं संयोजक गुणांक कैलकुलेटर इसके बारे में अधिक जानने के लिए और दिखाए गए सभी चरणों को देखकर अभ्यास करना।
सारांश का उपयोग करते हुए सामान्य द्विपद प्रमेय
उपरोक्त योग जो द्विपद प्रमेय को परिभाषित करता है, शब्दों को अधिक समझने योग्य बनाने के लिए विस्तार द्वारा संकेतन का उपयोग करता है। गणित में हमेशा की तरह, हम चीजों को और अधिक कॉम्पैक्ट बनाने की कोशिश करते हैं, और उपरोक्त अभिव्यक्ति को संक्षेप में प्रस्तुत किया जा सकता है:
\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]विस्तार में पदों की शक्तियों का निरीक्षण करें। सामान्य शब्द \(a^i b^{n-i}\) (एक स्थिर समय) है। शक्तियों का योग \(i + (n-i) = n\) है। तो विस्तार में सभी शर्तों की शक्तियों का योग \(n\) होना चाहिए। सुंदर है ना???
उदाहरण 1
क्या पद \(x^3 y^2\) (स्थिर का समय) \((x+y)^6\) के विस्तार का हिस्सा हो सकता है? क्यों?
उत्तर:
जवाब न है। इस मामले में, \(n = 6\), और हम द्विपद प्रमेय से जानते हैं कि विस्तार में \(x^l y^m\) पदों की शक्तियों का योग \(n\) के बराबर होना चाहिए। इस मामले में, \(l + m = 3 + 2 = 5\), जो \(n = 6\) के समान नहीं है। इसलिए, पद \(x^3 y^2\) (स्थिर का समय) \((x+y)^6\) के विस्तार का हिस्सा नहीं हो सकता है।
उदाहरण 2
द्विपद प्रमेय का उपयोग करके \((a-b)^3\) का विस्तार करें।
उत्तर:
रुकना। आप सोच रहे होंगे "आपने अभी मुझे \((a+b)^n\) का विस्तार करना सिखाया है, लेकिन अब आप मुझसे \((a-b)^n\) के बारे में पूछते हैं। आप इतने क्रूर क्यों हैं"। रुको। मैं तुम्हारे साथ कोई चाल नहीं चल रहा हूं।
हमेशा एक तरकीब होती है (उस लाइन को मत भूलना, यह मैथ में बहुत दिखाई देती है)।
ध्यान दें कि \(a - b\) \(a + (-b)\) के समान है।
अह्ह्ह्ह्ह, इसलिए द्विपद प्रमेय अभी भी लागू होता है। तो फिर:
\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]द्विपद विस्तार के बारे में अधिक जानकारी
द्विपद प्रमेय इतना महत्वपूर्ण है कि यह बीजगणित, कलन, संभाव्यता और सांख्यिकी सहित ज्यादातर सभी पाठ्यक्रमों में शामिल है।
नकारात्मक द्विपद विस्तार जैसे कुछ सामान्यीकरण हैं, जो इस ट्यूटोरियल के दायरे से बाहर हैं।
पास्कल त्रिभुज
कभी-कभी छात्र अटक जाते हैं जब उन्हें द्विपद विस्तार में जाने वाले स्थिरांक (संयोजन गुणांक) की गणना करने की आवश्यकता होती है। ऐसा करने का एक आसान तरीका पास्कल त्रिभुज का उपयोग करना है।
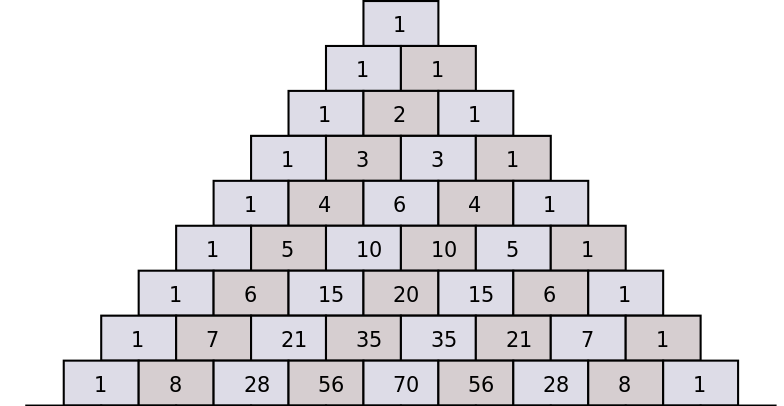
पास्कल त्रिभुज दिखाता है कि कैसे क्रमिक द्विपद गुणांकों की गणना \(n\) के पिछले मान के गुणांकों के आधार पर की जा सकती है, जो तुरंत ऊपर आने वाले दो गुणांकों को जोड़कर करते हैं।
अनुप्रयोग
द्विपद विस्तार में बीजगणित और संभाव्यता सिद्धांत में कई अनुप्रयोग हैं। उदाहरण के लिए, प्रायिकता में, द्विपद बंटन द्विपद प्रमेय पर आधारित होता है।
दरअसल, एक संख्या \(0 \le p \le 1\) पर विचार करें। फिर, \(p + (1-p) = 1\) और हम द्विपद प्रमेय का उपयोग कर सकते हैं:
\[\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} \]जिसका मतलब है कि
\[\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1 \]यह पता चला है कि प्रत्येक पद \({n \choose i} p^i (1-p)^{n-i}\) एक संभावना का प्रतिनिधित्व करता है। इसके अलावा, हमारे पास है:
\[\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1 \]जहां \(X\) \(n\) परीक्षणों के बाद सफलताओं की संख्या है, जब प्रत्येक परीक्षण की सफलता की संभावना \(p\) है। \(X\) चर को द्विपद यादृच्छिक चर के रूप में जाना जाता है।
संबंधित कैलकुलेटर
आप भी कर सकते हैं इस कैलकुलेटर का उपयोग करके द्विपद वितरण के लिए संभावनाओं की गणना करें . इसके अलावा, आप गणना करना चाह सकते हैं क्रमपरिवर्तन गुणांक , जो संयोजक गुणांक से संबंधित हैं।