गाउस विलोपन
गॉसियन एलिमिनेशन एक मैट्रिक्स को डालने के उद्देश्य से मैट्रिसेस पर आयोजित एक प्रक्रिया है सोपानक रूप . इस तरह के रूप में एक मैट्रिक्स होने से मैट्रिक्स समीकरणों को बहुत आसानी से हल करने में काफी मदद मिलती है।
तकनीकी रूप से, गाऊसी उन्मूलन की प्रक्रिया में एक धुरी के साथ एक स्तंभ (जो एक गैर-शून्य तत्व के लिए फैंसी स्लैंग है) को खोजने में शामिल है जो हमें धुरी के नीचे के सभी तत्वों को समाप्त करने की अनुमति देता है।
धुरी खोजने और समाप्त करने की यह प्रक्रिया हमें एक मैट्रिक्स को सोपानक रूप में रखने की अनुमति देती है, और जिस तरह से प्रक्रिया चलती है वह ऐसा है कि धुरी के द्वारा आप सोपानक रूप में एक नया स्तंभ जोड़ते हैं, और आप सोपानक रूप को 'बर्बाद' नहीं करते हैं। पिछले चरण तक बना लिया है। सुंदर अगर आप मुझसे पूछें।
शब्द "एखेलॉन फॉर्म" जो गॉसियन एलिमिनेशन का उपयोग करके प्राप्त किया जाता है, ऊपर दिए गए मैट्रिक्स को देखकर स्पष्ट हो जाता है, जहां मैट्रिक्स के गैर-शून्य तत्वों में यह सोपान जैसी संरचना होती है, जैसा कि लाल रेखा द्वारा दिखाया गया है।
धुरी और गाऊसी उन्मूलन के पीछे का गणित
हम इसमें बहुत अधिक तकनीकी नहीं होने जा रहे हैं, हम केवल यह प्रयास करने जा रहे हैं कि आप इस तरह के उन्मूलन की प्रेरणा और यांत्रिकी को समझें।
विचार एक मैट्रिक्स \(A\), आयाम \(m \times n\) (यह है, इसमें \(m\) पंक्तियाँ और \(n\) कॉलम हैं) को एक अलग रूप में प्राप्त करना है जो समीकरणों को हल करने के लिए अधिक उत्तरदायी है।
अधिक विशेष रूप से, एक \(m\times n\) मैट्रिक्स \(A\), और एक \(m\times 1\) वेक्टर \(b\) के लिए, हमें एक \(n\times 1\) वेक्टर \(x\) खोजने की आवश्यकता है जैसे कि
\[Ax = b\]आप सोच सकते हैं, "यह इतना आसान है, हम प्रत्येक पक्ष को बाईं ओर से \(A^{-1}\) से गुणा करते हैं" इसलिए हमें यह प्राप्त होता है:
\[x = A^{-1} b \]....इतना शीघ्र नही! यह तभी काम करता है जब मैट्रिक्स \(A\) उलटा हो। शुरू करने के लिए, मैट्रिक्स \(A\) को एक वर्ग मैट्रिक्स होना चाहिए, और फिर, इसके निर्धारक को शून्य से अलग होना चाहिए। लेकिन आप गैर-वर्ग मैट्रिक्स के लिए व्युत्क्रम से गुणा नहीं कर सकते। तो, फिर आप इसे कैसे करते हैं?
आपको समीकरण को हल करने में आसान एक में बदलने की जरूरत है।
विशेष रूप से, सोपानक रूप में मैट्रिसेस ऐसे मेट्रिसेस होते हैं जो ऐसे समीकरणों की ओर ले जाते हैं जिन्हें हल करना आसान होता है (इसके बारे में बाद में)।
प्राथमिक मैट्रिक्स का उपयोग करना
सबसे पहले, हम एक महत्वपूर्ण नोट करेंगे। यदि हमारे पास मैट्रिक्स समीकरण \(Ax = b\) का समाधान है, और \(E\) एक उलटा मैट्रिक्स है, तो \(x\) भी \((EA)x = Eb\) का समाधान है, और इसके विपरीत।
दूसरे शब्दों में, मैट्रिक्स समीकरण
\[Ax = b\]तथा
\[(EA)x = Eb\]व्युत्क्रमणीय मैट्रिक्स \(E\) के समतुल्य हैं। इससे हमारा क्या तात्पर्य है कि समीकरण समतुल्य हैं? हमारा मतलब है कि समीकरणों के समान हल होते हैं।
तो हम जो करने जा रहे हैं वह \(Ax = b\) से शुरू करना है, और इनवर्टिबल मैट्रिसेस \(E\) से गुणा करके, हम एक समकक्ष मैट्रिक्स समीकरण पर पहुंचने जा रहे हैं जो है हल करना बहुत आसान है .
मान लें कि हम इनवर्टिबल मैट्रिसेस \(E_1, E_2, ..., E_n\) की एक सूची खोजने में सक्षम हैं और हम मूल मैट्रिक्स समीकरण को एक समान समीकरण में बदलने के लिए (बाएं से) गुणा करते हैं, जैसे:
\[Ax = b \,\,\,\, \Leftrightarrow \,\,\,\, (E_1 \cdot A)x = (E_1 \cdot b)\] \[... \Leftrightarrow \,\,\,\, (E_n \cdots E_2 \cdot E_1 \cdot A)x = (E_n \cdots E_2 \cdot E_1 \cdot b)\] \[ \Leftrightarrow \,\,\,\, \tilde A x = \tilde b\]जहां \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde A\) और \(E_n \cdots E_2 \cdot E_1 \cdot A = \tilde b\)।
हमारा उद्देश्य सावधानी से करना है चुनें उलटा मैट्रिक्स \(E_1, E_2, ..., E_n\) ताकि \(\tilde A\) सोपानक रूप में हो।
ऐसा क्यों है? क्योंकि अगर \(\tilde A\) सोपानक रूप में है, तो मैट्रिक्स समीकरण \(\tilde A x = \tilde b\) को हल करना बहुत आसान है, और हम पहले से ही जानते हैं कि \(\tilde A x = \tilde b\) के \(A x = b\) के समान समाधान हैं।
उदाहरण 1
आइए देखें कि मैट्रिक्स समीकरण को हल करना इतना आसान क्यों है जब आपके पास यह सोपानक रूप में होता है। पहले कल्पना करें कि आपके पास निम्नलिखित मैट्रिक्स और वेक्टर हैं:
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & -1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]और आप \(Ax = b\) को हल करना चाहते हैं। समीकरणों की प्रणाली कैसी दिखेगी? सिस्टम \(Ax = b\) ऐसा दिखेगा
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 - x_3 = 1\]ये कैसा दिखाई देता है? अच्छा, इतना साफ-सुथरा नहीं। आपको समीकरणों की बाजीगरी शुरू करनी होगी। उन्मूलन जैसी चीजों का उपयोग करके इसे हल करने के लिए कमोबेश व्यवस्थित दृष्टिकोण हैं, लेकिन यह कम से कम बोझिल है।
अब, दूसरी ओर, कल्पना करें कि आपके पास निम्नलिखित मैट्रिक्स और वेक्टर हैं:
\[\tilde A = \left[ \begin{matrix} -1 & 1 & 1 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \\ \end{matrix} \right] \] \[\tilde b= \left[ \begin{matrix} 1 \\ -1 \\ -1 \\ \end{matrix} \right]\]और आप \(\tilde A x = \tilde b\) को हल करना चाहते हैं। इस मामले में, मैट्रिक्स \(\tilde A\) सोपानक रूप में है। समीकरणों की प्रणाली कैसी दिखेगी? सिस्टम \(\tilde A x = \tilde b\) ऐसा दिखेगा
\[-x_1 + x_2 + x_3 = 1\] \[x_2 - x_3 = -1\] \[x_3 = -1\]यह कैसा दिखता है? खैर, ज्यादा जर्जर नहीं।
दरअसल, अगर हम सीधे तीसरे समीकरण से शुरू करते हैं, तो हमारे पास सीधे \(x_3 = -1\) होता है। फिर दूसरे समीकरण से, \(x_2 = -1 + x_3 = -1 + (-1) = -2\)। और पहले समीकरण से, \(x_1 = x_2 + x_3 -1 = -2 + (-1) - 1 = -4\)। तो बिना किसी फ़ज़ के, हमने पाया है कि:
\[x_1 = -4, \, x_2 = -2, x_3 = -1\]इसलिए, इस मामले में सिस्टम को तुच्छ रूप से हल किया जाता है।
सोपानक रूप में मैट्रिसेस से जुड़ी प्रणालियों के लिए, समाधान प्राप्त करने के लिए अंतिम समीकरण से पहले समीकरण पर वापस जाना सीधा है।
सही उलटा मैट्रिक्स कैसे चुनें
अब जब हम जानते हैं कि सोपानक रूप में मैट्रिसेस के साथ काम करना मैट्रिक्स समीकरणों को हल करना वास्तव में बहुत आसान बनाता है, तो हमें आश्चर्य होना चाहिए कि ऐसे कौन से इनवर्टिबल मैट्रिसेस \(E_1, E_2, ..., E_n\) हैं जो \(\tilde A\) को सोपानक रूप में बनाएंगे।
गाऊसी उन्मूलन कैसे काम करता है?
दिलचस्प बात यह है कि इन आव्यूहों \(E_1, E_2, ..., E_n\) को खोजना कठिन नहीं है, जिन्हें प्राथमिक आव्यूह कहा जाएगा।
चरण 1
: पहले कॉलम को देखें, अगर उसका नॉन-जीरो वैल्यू है, तो वह आपका पिवट होगा। यदि पहले कॉलम की पहली पंक्ति गैर-शून्य है, तो इसे पिवट के रूप में उपयोग करें। यदि नहीं, तो एक ऐसी पंक्ति खोजें, जिसमें एक गैर-शून्य मान हो और उस पंक्ति और पहली पंक्ति को क्रमित करें।
तो, आपको एक धुरी मिलती है, और संभावित रूप से आपको एक पंक्ति क्रमपरिवर्तन करने की आवश्यकता होती है (जिसे वास्तव में एक निश्चित एक उलटा मैट्रिक्स द्वारा गुणा करके दर्शाया जाता है)
चरण 2
: एक बार जब आपके पास पिवट हो जाए, तो पिवट के नीचे, वर्तमान कॉलम के सभी तत्वों को हटा दें।
यह पिवट पंक्ति को एक निश्चित स्थिरांक से गुणा करके, और इसे पिवट के नीचे एक पंक्ति में जोड़कर किया जाता है, ताकि पिवट के समान कॉलम में तत्व शून्य हो जाए।
चरण 3
: एक बार जब धुरी के नीचे के सभी तत्वों को उपयुक्त पंक्ति संचालन (जो एक उलटा मैट्रिक्स के संचालन द्वारा दर्शाया जाता है) बनाकर शून्य बना दिया गया है, अगले कॉलम, अगली पंक्ति पर जाएं, और नीचे की पंक्ति से एक पिवट की तलाश करें। पिछली धुरी की पंक्ति से और उसी प्रक्रिया को करें।
चरण 4
: तब तक दोहराएं जब तक कि आपके कॉलम समाप्त न हो जाएं या मैट्रिक्स सोपानक रूप में न हो जाए।
उदाहरण 2
धुरी और गाऊसी उन्मूलन का उपयोग करते हुए, निम्नलिखित प्रणाली को हल करें:
\[x_1 + x_2 + x_3 = 2\] \[x_1 - x_2 + x_3 = 1\] \[-x_1 + x_2 + x_3 = 1\]उत्तर:
सबसे पहले, संबंधित मैट्रिक्स \(A\) और वेक्टर \(b\) हैं:
\[A= \left[ \begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ -1 & 1 & 1 \\ \end{matrix} \right]\] \[b= \left[ \begin{matrix} 2 \\ 1 \\ 1 \\ \end{matrix} \right]\]संवर्धित मैट्रिक्स \([A|b]\) है
\[\left[ \begin{matrix} 1 & 1 & 1 & 2 \\ 1 & -1 & 1 & 1 \\ -1 & 1 & 1 & 1 \\ \end{matrix} \right]\]सिस्टम को हल करने के लिए, हमें गॉसियन एलिमिनेशन जाना होगा। हम पहले कॉलम से शुरू करते हुए, पहला पिवट चुनते हैं। पहले कॉलम की पहली पंक्ति में तत्व 1 है, जो शून्य से अलग है और फिर, इसे पिवट के रूप में प्रयोग किया जाता है। हम उस धुरी (1) का उपयोग उसके नीचे के सभी तत्वों को समाप्त करने के लिए करते हैं:
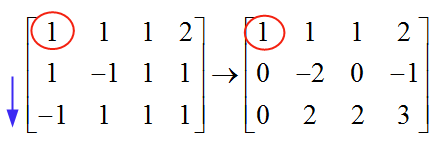
धुरी के नीचे के तत्वों को खत्म करने की क्रियाविधि सरल है। इस मामले में, पिवट के नीचे "1" को खत्म करने के लिए, मैं पंक्ति 1 में तत्वों को पंक्ति 2 में तत्वों से घटाता हूं। इस तरह मैं धुरी के नीचे एक शून्य बनाता हूं।
इसी तरह, पंक्ति 3 में "-1" को खत्म करने के लिए, मैं पंक्ति 1 में तत्वों को पंक्ति 3 में तत्वों में जोड़ता हूं। इस तरह मैं पंक्ति 3 में पिवट के नीचे एक शून्य बनाता हूं।
हम देखेंगे कि यह पंक्ति संचालन उलटा मैट्रिक्स द्वारा गुणा करके प्राप्त किया जाता है, इसलिए हमारे पास ऐसा करने से समकक्ष सिस्टम होते हैं।
अब, अगली पंक्ति, अगले कॉलम में जाने पर, हमें एक "-2" मिलता है, जो शून्य से भिन्न होता है, और इसलिए, इसे हमारी धुरी के रूप में उपयोग किया जाता है। इस धुरी के नीचे के मान को समाप्त करने के लिए, हम पंक्ति 3 में पंक्ति 2 के मान जोड़ते हैं:
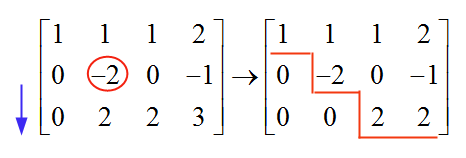
और अब हम रुकते हैं, क्योंकि परिणामी मैट्रिक्स पहले से ही सोपानक रूप में है। अब हम सिस्टम को हल करने के लिए बैक-ट्रैक करते हैं:
\[2x_3 = 2 \,\,\,\, \Rightarrow \,\,\,\, x_3 = 1\] \[-2x_2 = -1 \,\,\,\, \Rightarrow \,\,\,\, x_2 = 1/2\] \[x_1+x_2+x_3 = 1 \,\,\,\, \Rightarrow \,\,\,\, x_1 = 1 - x_2 - x_3 = 1 - 1/2 - 1 = -1/2\]गाऊसी उन्मूलन के बारे में अधिक
रेखीय प्रणालियों को हल करने के लिए धुरी उन्मूलन और धुरी उन्मूलन का उपयोग आधारशिला है। लेकिन यह उससे आगे निकल जाता है। यदि हम केवल रैखिक प्रणालियों की परवाह करते हैं, तो हम उपयोग करेंगे क्रैमर का नियम , जो के लिए ठीक काम करता है समाधान प्रणाली .
गाऊसी उन्मूलन का लाभ यह है कि यह मैट्रिक्स को पंक्ति सोपानक तरीके से डालने का एक व्यवस्थित तरीका देता है, जो बदले में कुछ मैट्रिक्स अपघटनों (एलयू, एलडीयू, आदि) की त्वरित प्राप्ति की ओर जाता है, या यहां तक कि मैट्रिक्स के व्युत्क्रम की गणना के लिए भी। .
क्रमचय के प्राथमिक मैट्रिक्स
सामान्य अभिव्यक्तियों को कारक बनाने के लिए कोई सामान्य नियम नहीं हैं। हमें कान से खेलने और अभिव्यक्ति की संरचना का फायदा उठाने की कोशिश करने की जरूरत है। कभी-कभी हम कारक कर सकते हैं, कभी-कभी हम नहीं कर सकते। यह सब अभिव्यक्ति पर निर्भर करता है। एकमात्र सामान्य नियम समूह बनाने का प्रयास करना है और सामान्य कारकों को खोजने का प्रयास करना है ताकि आगे समूह और सरल बनाया जा सके।
पंक्ति संचालन के प्राथमिक मैट्रिक्स
समाधान खोजने के लिए पिवट विधि की कुंजी यह है कि क्रमपरिवर्तन और पंक्ति संचालन व्युत्क्रमणीय मैट्रिसेस हैं, इसलिए जिस प्रणाली को हम प्रत्येक चरण में बदल रहे हैं वह मूल प्रणाली के बराबर है।
दरअसल, पंक्तियों और पंक्ति संचालन के क्रमपरिवर्तन दोनों को व्युत्क्रम मैट्रिक्स द्वारा दर्शाया जाता है। मैट्रिक्स \(E_{ij}\) पर विचार करें, जो पहचान मैट्रिक्स \(I\) लेकर और इसकी पंक्तियों \(i\) और \(j\) को क्रमित करके प्राप्त किया जाता है।
मैट्रिक्स \(E_{ij}\) को बाईं ओर से किसी भी मैट्रिक्स \(A\) से गुणा करने का प्रभाव \(A\) की पंक्तियों \(i\) और \(j\) को प्राप्त करना है।
अब \(i < j\) के लिए मैट्रिक्स \(E_{ij}^{\lambda}\) पर विचार करें, जो पंक्ति \(i\) को छोड़कर, सभी पंक्तियों के लिए पहचान मैट्रिक्स से मेल खाती है, जहां i का मान वां कॉलम 0 के बजाय \(\lambda\) है।
कॉलम के साथ संचालन के बारे में कैसे?
कभी-कभी हमें पिवट खोजने के लिए स्तंभों को क्रमपरिवर्तन करने की आवश्यकता होती है। उस स्थिति में हमें मैट्रिक्स \(E_{ij}\) को दाईं ओर से गुणा करने की आवश्यकता है, और परिणाम \(A\) के कॉलम \(i\) और \(j\) प्राप्त करने के लिए होगा।