क्रैमर का नियम
क्रेमर का नियम एक तकनीक है जिसका उपयोग निर्धारकों की गणना के आधार पर रैखिक समीकरणों की प्रणालियों को व्यवस्थित रूप से हल करने के लिए किया जाता है।
आमतौर पर, हल करना रैखिक समीकरणों की प्रणाली 2x2 से बड़े सिस्टम के लिए गन्दा हो सकता है, क्योंकि तीन या अधिक चर होने पर इसे कम करने के कई तरीके हैं।
क्रैमर का नियम रैखिक समीकरणों की प्रणालियों के समाधान खोजने का स्पष्ट, व्यवस्थित तरीका प्रदान करता है, चाहे सिस्टम का आकार कोई भी हो।
बड़ी प्रणालियों के लिए आवश्यक गणनाओं की संख्या में वृद्धि होती है, लेकिन प्रणाली के आकार की परवाह किए बिना प्रक्रिया बिल्कुल समान होती है।
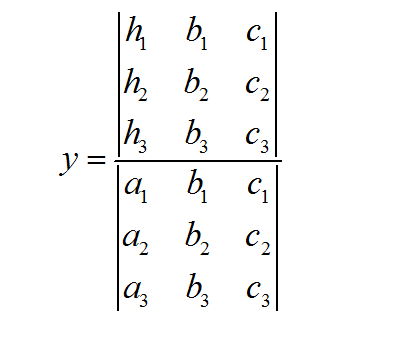
क्रैमर के नियम का उपयोग कैसे करें
चीजों को आसान बनाने के लिए, हम \(n = 2\) के मामले पर काम करेंगे और फिर हम एक अधिक सामान्य संस्करण स्थापित करेंगे, जो उम्मीद है कि \(n=2\) मामले से निपटने के बाद बेहतर समझ में आएगा।
चरण 1
: सभी 2x2 रैखिक प्रणालियों को निम्नलिखित रूप में लिखा जा सकता है:
तो आपका पहला कदम इन मानों को ढूंढ रहा है \(a_1, b_1, c_1\) तथा \(a_2, b_2, c_2\) उस सिस्टम के लिए जिसे आप हल करना चाहते हैं।
चरण 2
: एक बार जब आपके पास गुणांक \(a_1, b_1, c_1\) और \(a_2, b_2, c_2\) हो, तो आप \(x\) और \(y\) को हल करने के लिए निम्नलिखित सूत्रों का उपयोग करते हैं:
उपरोक्त सूत्र में, जहां यह "det" कहता है, इसका अर्थ संबंधित मैट्रिक्स का निर्धारक है। कभी-कभी, निर्धारकों के लिए अधिक कॉम्पैक्ट नोटेशन का उपयोग किया जाता है, जैसा कि नीचे दिखाया गया है:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]तो, उपरोक्त संकेतन का उपयोग करके, हमें क्रैमर के नियम के लिए ये अधिक कॉम्पैक्ट सूत्र प्राप्त होंगे:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]आइए हम यह समझने का एक दृश्य तरीका देखें कि क्या हो रहा है। ध्यान दें कि \(x\) और \(y\) दोनों के हर में एक ही सारणिक है।
हर में प्रयुक्त उस सामान्य मैट्रिक्स के गुणांक सीधे उन गुणांकों से प्राप्त होते हैं जो सिस्टम में \(x\) और \(y\) गुणा करते हैं। नीचे दी गई छवि देखें:
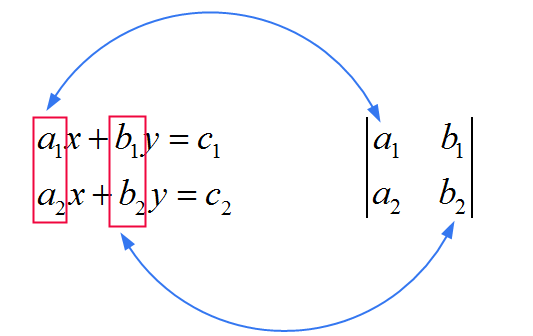
अब हम देखते हैं कि \(x\) और \(y\) उनके अंश में भिन्न हैं। नियम को याद रखने के तरीके के रूप में, इस पर विचार करें:
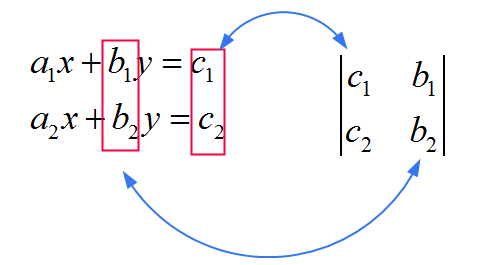
\(x\) के लिए, आप समान मैट्रिक्स का उपयोग हर में एक के रूप में करते हैं, केवल यह कि आप पहले कॉलम को गुणांक \(c_1\) और \(c_2\) के साथ प्रतिस्थापित करते हैं। नीचे दी गई छवि देखें
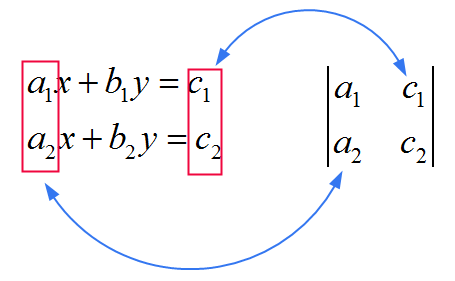
\(y\) के लिए, आप समान मैट्रिक्स का उपयोग हर में एक के रूप में करते हैं, केवल यह कि आप दूसरे कॉलम को गुणांक \(c_1\) और \(c_2\) से बदल देते हैं। नीचे दी गई छवि देखें
उदाहरण 1
निम्नलिखित 2x2 रैखिक प्रणाली को हल करें:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]उत्तर:
आइए ऊपर दिए गए सिस्टम को हल करने के लिए क्रैमर के नियम का उपयोग करने के लिए ऊपर बताए गए दो चरणों का पालन करें:
चरण 1
: हमें संबंधित निर्धारकों के लिए गुणांकों की पहचान करने की आवश्यकता है।
हर में जाने वाले मैट्रिक्स के लिए हम उपयोग करते हैं
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]अब, इस मामले में \(c_1 = 10, c_2 = 4\), \(x\) की गणना करने के लिए उपयोग किए जाने वाले निर्धारक के लिए, हम पहले कॉलम को बदलकर पिछले मैट्रिक्स को बदलते हैं:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]\(y\) की गणना करने के लिए उपयोग किए जाने वाले निर्धारक के लिए हम दूसरे कॉलम को बदलकर पिछले मैट्रिक्स को बदलते हैं:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]तो अब हमें समाधान मिलता है:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]और \(y\) के लिए:
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]इसलिए, समाधान \(x = 3\), \(y = 1/2\) है।
सामान्य मामले के लिए क्रैमर नियम
क्रैमर के नियम की खूबी यह है कि यह ठीक उसी प्रक्रिया को लागू करता है, चाहे वह 2x2 प्रणाली हो या 10x10 प्रणाली हो। अवधारणा वही है।
तो, मान लें कि \(x_1, x_2, ..., x_n\) चर (अज्ञात) हैं, और हम रैखिक समीकरणों की निम्नलिखित nxn प्रणाली को हल करना चाहते हैं:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]\(x_1, x_2, ..., x_n\) को हल करने के लिए, हम हर पर निम्नलिखित सारणिक का उपयोग करेंगे:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• \(x_1\) का समाधान है
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• \(x_2\) का समाधान है
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]और इसी तरह। जैसा कि आप देख सकते हैं, हर में सारणिक समान है, और अंश में एक \(x_1\) के लिए \((c_1, ..., c_n)\) के साथ पहले कॉलम को बदलकर प्राप्त किया जाता है। \(x_2\) के लिए हम दूसरे कॉलम को \((c_1, ..., c_n)\) से बदलते हैं, \(x_3\) के लिए हम तीसरे कॉलम को बदलते हैं, इत्यादि। तुम्हें नया तरीका मिल गया है।
उदाहरण 2
क्रैमर नियम का उपयोग करके 3x3 रैखिक समीकरणों की निम्नलिखित प्रणाली को हल करें।
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]उत्तर:
सबसे पहले, हम हर में जाने वाले सारणिक की पहचान करते हैं:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]इसके अलावा, हमें \(c_i\) गुणांक के वेक्टर की पहचान करने की आवश्यकता है:
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]यह सदिश वह होगा जो हर से उभयनिष्ठ निर्धारक के संगत स्तंभों को प्रतिस्थापित करेगा। हम पाते हैं:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]क्रैमर नियम के बारे में अधिक जानकारी
रैखिक समीकरणों की प्रणालियों को कुशलतापूर्वक हल करने में क्रैमर के नियम की एक विशिष्ट भूमिका है। इसमें निर्धारकों का उपयोग बहुत सीधा कार्य करने के लिए शामिल है जो अन्यथा वास्तव में जटिल होगा, खासकर बड़ी प्रणालियों के लिए।
अंततः, करने के लिए रैखिक प्रणालियों को हल करें , आपको बस इतना करना है कि सिस्टम के आधार पर एक संख्या मैट्रिक्स निर्धारकों की पहचान करें जिन्हें हल करने की आवश्यकता है, और सिस्टम को हल करने के लिए एक सरल बीजगणितीय संचालन का संचालन करें।
अनुप्रयोग
क्रैमर के नियम में रैखिक बीजगणित और विभेदक समीकरण दोनों में कई अनुप्रयोग हैं।