الجبر دروس

نظرية ذات الحدين

نظرية ذات الحدين هي واحدة من أكثر النظريات شهرة في الجبر , ولها العديد من التطبيقات في مجالات الجبر والاحتمالات والإحصاء. تنص على صيغة لطيفة وموجزة لـ n ^ذ قوة مجموع قيمتين: \((a+b)^n\)

تم تقديمي لأول مرة بشكل غير رسمي من قبل السير إسحاق نيوتن في عام 1665.

عالج العديد من علماء الرياضيات البارزين نظرية ذات الحدين بعد نيوتن. لقد كانت مشكلة جذابة للغاية في القرنين السابع عشر والثامن عشر.

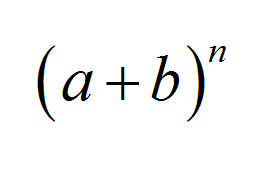
صيغة التوسع ذي الحدين

ما هو العدد الصحيح حول نظرية ذات الحدين هو أنه يوفر صيغة أنيقة وموجزة للغاية. قبل الدخول في الصيغة , دعونا نجري بعض العمليات الحسابية. على سبيل المثال , بالنسبة إلى \(n = 2\) نحصل على:

\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]

لنجرب الآن مع \(n = 3\):

\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]

أخيرًا , دعونا نتحلى بالشجاعة ونجربها مع \(n = 4\):

\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]

حسنًا , كان ذلك شجاعًا , أليس كذلك؟ هل ترى أي أنماط هناك. أستطيع أن أرى البعض. على سبيل المثال , بالنسبة إلى \(n = 2\) يمكننا تبسيطها إلى 3 مصطلحات. بالنسبة إلى \(n = 3\) يمكننا تبسيطها إلى 4 مصطلحات , وبالنسبة إلى \(n = 4\) يمكننا تبسيطها إلى 5 مصطلحات. لذلك بشكل عام , أتوقع أنه بالنسبة للسلطة العامة لـ \(n\) , سيكون لدينا شروط \(n+1\)

المزيد من الأنماط؟ حسنًا , هناك دائمًا مصطلح من النموذج \(a^l b^m\) , ويمكننا أن نرى أن قوى \(l\) تتناقص , وتزداد القوى \(m\). ولكن هناك شيء مثير للاهتمام أيضًا: إذا قمت بفحص كل مصطلح , فسيكون مجموع القوى دائمًا \(n\). في الواقع , سوف تتحقق من أن \(l + m = n\) لجميع هذه الشروط.

على سبيل المثال , بالنسبة إلى \(n = 2\) لديك المصطلح \(2 a b\). قوة \(a\) تساوي 1 وقوة \(b\) تساوي 1 ومجموع القوى \(1 + 1 = 2\). أو على سبيل المثال , بالنسبة إلى \(n = 4\) , لديك المصطلح \(6 a^2 b^2\) , حيث قوة \(a\) تساوي 2 , وقوة \(b\) تساوي 2 , ومجموع القوى هو \(2 + 2 = 4\)

النظرية العامة ذات الحدين

نحن الآن جاهزون لإعطاء التعبير العام لنظرية ذات الحدين. مستعد؟ نملك:

\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]

حيث يُقرأ المصطلح \({n \choose i}\) على أنه "n اختر i" أو أيضًا على أنه "معامل اندماجي" , ويتم تعريفه على أنه

\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]

على سبيل المثال,

\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]

يمكنك استخدام هذا حاسبة معامل اندماجي لمعرفة المزيد عنها والممارسة من خلال رؤية جميع الخطوات الموضحة.

النظرية العامة ذات الحدين باستخدام الجمع

يستخدم المجموع أعلاه الذي يحدد نظرية ذات الحدين الترميز بالامتداد , لجعل المصطلحات أكثر قابلية للفهم. كما هو الحال دائمًا في الرياضيات , نحاول أن نجعل الأشياء أكثر إحكاما , ويمكن تلخيص التعبير أعلاه على النحو التالي:

\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]

لاحظ قوى المصطلحات في التوسيع. المصطلح العام هو \(a^i b^{n-i}\) (عدد مرات ثابت). مجموع القوى \(i + (n-i) = n\). لذا يجب أن يكون مجموع قوى ALL في التوسع \(n\). أليست جميلة ؟؟؟

مثال 1

هل يمكن للمصطلح \(x^3 y^2\) (عدد مرات ثابت) أن يكون جزءًا من توسيع \((x+y)^6\)؟ لماذا ا؟

إجابه:

الجواب لا. في هذه الحالة , \(n = 6\) , ونعلم من نظرية ذات الحدين أن مجموع قوى المصطلحات \(x^l y^m\) في التوسيع يجب أن يساوي \(n\). في هذه الحالة , \(l + m = 3 + 2 = 5\) , والتي تختلف عن \(n = 6\). ومن ثم , فإن المصطلح \(x^3 y^2\) (مرات ثابت) لا يمكن أن يكون جزءًا من توسيع \((x+y)^6\).

مثال 2

قم بتوسيع \((a-b)^3\) باستخدام نظرية ذات الحدين.

إجابه:

انتظر. لا بد أنك تفكر "لقد علمتني للتو كيفية توسيع \((a+b)^n\) , ولكن الآن تسألني عن \((a-b)^n\). لماذا أنت قاسي جدًا". يتمسك. أنا لا ألعب عليك الحيل.

هناك دائمًا خدعة (لا تنس هذا السطر , فهو يظهر كثيرًا في الرياضيات).

لاحظ أن \(a - b\) هو نفسه \(a + (-b)\).

Ahhhhhhh , لذلك لا تزال نظرية ذات الحدين سارية. وماذا بعد:

\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]

المزيد عن التوسع ذي الحدين

تعتبر نظرية ذات الحدين مهمة للغاية , حيث يتم تناولها في الغالب في جميع الدورات بما في ذلك الجبر وحساب التفاضل والتكامل والاحتمالية والإحصاء.

هناك بعض التعميمات مثل التوسيع السلبي ذي الحدين , والذي يتجاوز نطاق هذا البرنامج التعليمي.

مثلث باسكال

يتعثر الطلاب في بعض الأحيان عندما يحتاجون إلى حساب الثوابت (المعاملات الاندماجية) التي تدخل في التوسع ذي الحدين. إحدى الطرق السهلة للقيام بذلك هي استخدام مثلث باسكال.

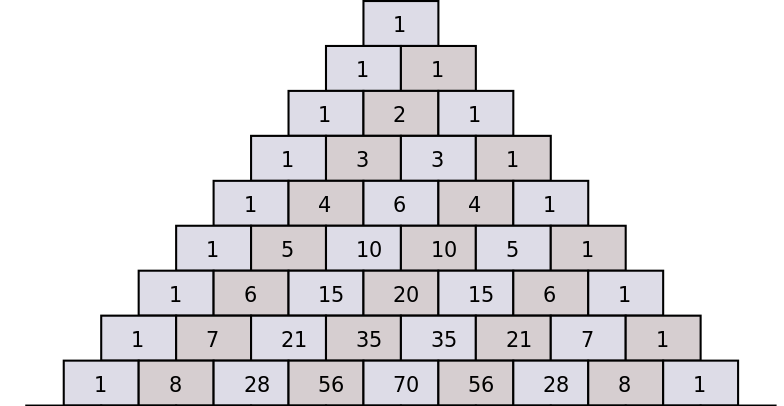
يوضح مثلث باسكال كيف يمكن حساب المعاملات ذات الحدين المتتالية بناءً على معاملات القيمة السابقة لـ \(n\) , عن طريق إضافة المعاملين اللذين يأتيان أعلاه مباشرة.