متباينات القيمة المطلقة
عدم المساواة في القيمة المطلقة هي عدم المساواة التي يوجد فيها واحد أو أكثر قيمه مطلقه . لنتذكر أن المتباينة تشبه المعادلة تقريبًا , ولكن بدلاً من علامة "=" , لدينا "≤" أو "≥".
هذا الاختلاف يجعل مجموعة الحلول عادةً منطقة , كما هو الحال في معظم المتباينات. وحقيقة أن هناك قيمًا مطلقة تشير إلى معاملة خاصة معينة لحلها.
في هذا البرنامج التعليمي سوف نركز على المهارات المحددة المطلوبة لحل هذا النوع من عدم المساواة الذي يحتوي على خام واحد أكثر من القيم المطلقة. أيضًا , سنفترض أن متغيرًا واحدًا أو متغيرين , \(x\) و / أو \(y\) متورطان في المتباينة.
ما هو عدم المساواة في القيمة المطلقة؟
لغرض هذا التحليل , سنعتبر أن متباينة القيمة المطلقة هي متباينة تتضمن متغيرًا واحدًا أو متغيرين , مع قيمة مطلقة واحدة على الأقل.
على سبيل المثال , لدينا أدناه تفاوت في القيمة المطلقة بمتغيرين \(x\) و \(y\):
\[|3x+2y-1| \ge 1\]أو أيضًا , يمكن أن يكون لدينا متباينة القيمة المطلقة التالية بمتغير واحد فقط:
\[|3x-1| \le 2\]لأغراضنا , ولغرض التقنيات المستخدمة لحلها , سنتعامل مع كلا النوعين من عدم المساواة (متغير واحد ومتغيران)
كيفية حل عدم المساواة في القيمة المطلقة؟
عند حل المعادلات أو عدم المساواة , ليس هناك حقًا حل سحري يحل كل شيء. كل مشكلة مختلفة وقد يكون لها خصائصها الخاصة.
أفضل ما يمكننا فعله هو تقديم سلسلة من الخطوات التي ستساعدك في عملية حل مشكلة عدم المساواة.
الخطوة 1:
لكل مطلقة تحديد المناطق التي تكون فيها حجة القيمة المطلقة سالبة وحيث تكون غير سالبة.
الخطوة 2:
إذا كانت هناك قيمة مطلقة واحدة فقط في المتباينة , فقم بحلها في كلا المجالين (حيث تكون وسيطة القيمة المطلقة سالبة وحيث تكون غير سالبة).
الخطوه 3:
إذا كان هناك أكثر من قيمة مطلقة في المتباينة , فأنت بحاجة إلى تقاطع كل المناطق للحصول على مجموعة من الأقسام الأصغر. في كل قسم , يجب أن تعرف بالضبط علامة كل وسيطة. ثم حل المتباينة في جميع المجالات.
الخطوة الرابعة:
بمجرد حصولك على حل الجزء الموجود في كل منطقة , فإن الحل النهائي هو ببساطة اتحاد هذه الحلول الجزئية.
بكلمات بسيطة: تحتاج إلى معرفة المناطق التي تعرف فيها بالضبط علامة وسيطة القيم المطلقة (حتى تتمكن من التخلص منها).
يجب أن يوضح زوجان من الأمثلة هذه الخطوات.
مثال 1
حل المتباينة التالية
\[| 2x + 4y - 1 | \ge 2\]إجابه:
لحل المتباينة , علينا استخدام الخطوات المحددة أعلاه.
الخطوة 1: هناك قيمة مطلقة واحدة فقط , لذا علينا تحديد ما إذا كانت الوسيطة سالبة وغير سالبة. لذلك , نحتاج إلى الحل أولاً:
\[2x + 4y - 1 \ge 0\]توجد عدة استراتيجيات لحل ما سبق , لكن أسهلها هو حل المعادلة أولاً
\[2x + 4y - 1 = 0\]مما يعني أن \(4y = -2x + 1\) أو نفس \(y = -\frac{1}{2}x + \frac{1}{4}\) , والذي يتوافق مع خط بميل \(m = -\frac{1}{2}\) وتقاطع ص \(n = \frac{1}{4}\).
الآن , لرعاية \(2x + 4y - 1 \ge 0\) , نختبر ما إذا كانت النقطة \((0,0)\) ترضي عدم المساواة أم لا:
\[2(0) + 4(0) - 1 = -1 < 0\]لذا , \((0,0)\) يرضي أو لا يرضي المتباينة. الاستنتاج هو أن الخط ذو المنحدر \(m = -\frac{1}{2}\) وتقاطع y \(n = \frac{1}{4}\) يقسم المستوى إلى منطقتين:
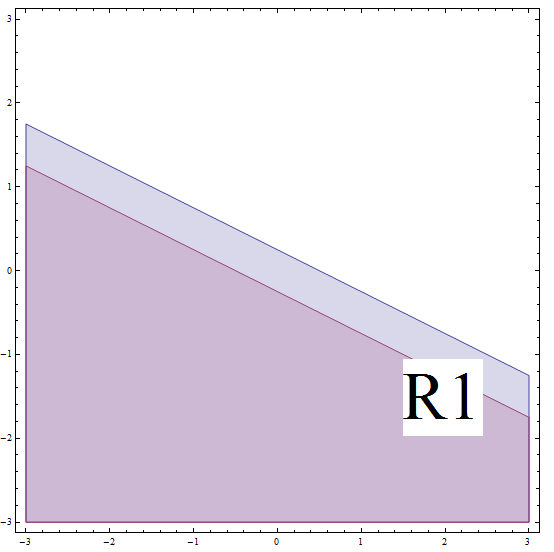
بالنسبة للنقاط الموجودة أسفل الخط (نسمي هذه المنطقة 1 , \(R_1\)) , نحصل على \(2x + 4y - 1 < 0\)
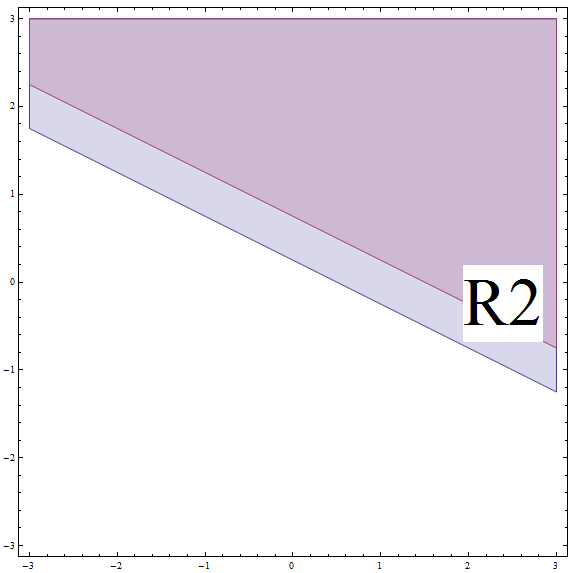
بالنسبة للنقاط الموجودة فوق الخط , بما في ذلك السطر نفسه (نسمي هذه المنطقة 2 , \(R_2\)) نحصل على \(2x + 4y - 1 \ge 0\)
لماذا هذا مهم؟ لماذا نأخذ كل هذه المشاكل؟ لأنه في \(R_1\) , حصلنا على ذلك منذ \( 2x + 4y - 1 < 0\) , ثم \(| 2x + 4y - 1 | = -(2x + 4y - 1) \). وبالمثل , في \(R_2\) , نحصل على ذلك منذ \( 2x + 4y - 1 \ge 0\) , ثم \(| 2x + 4y - 1 | = 2x + 4y - 1 \).
الخطوة 2: الآن نحن بحاجة إلى حل المتباينة في المنطقة 1 , \(R_1\) :
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]هذا يتوافق مع جميع النقاط الموجودة أسفل أو على الخط ذي المنحدر \(m = -\frac{1}{2}\) وتقاطع y \(n = -\frac{1}{4}\). لكن لا تنس أنك في \(R_1\) , وهذا السطر الذي وجدناه أدناه هو حد \(R_1\) (انظر الرسم البياني أدناه).
للتوضيح , نظرًا لأننا نفترض أننا في \(R_1\) , نحتاج إلى أن نكون خطًا أدنى من المنحدر \(m = -\frac{1}{2}\) وتقاطع y \(n = \frac{1}{4}\). في ظل هذا الافتراض , حللنا المتباينة الأصلية ونحتاج أيضًا إلى أن نكون تحت الخط مع الميل \(m = -\frac{1}{2}\) وتقاطع y \(n = -\frac{1}{4}\). يجب أن يحدث هذان الشرطان في وقت واحد , لذلك نحصل على تقاطع المنطقتين.
إذن , حل الجزء في هذه الحالة يتوافق مع جميع النقاط الموجودة أسفل أو على الخط ذي المنحدر \(m = -\frac{1}{2}\) وتقاطع y \(n = -\frac{1}{4}\).
الآن نحن بحاجة إلى حل المتباينة في المنطقة 2 , \(R_2\) :
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]هذا يتوافق مع جميع النقاط أعلاه أو على الخط ذي المنحدر \(m = -\frac{1}{2}\) وتقاطع y \(n = \frac{3}{4}\). لكن لا تنس أنك في \(R_2\) , وهذا السطر هو ABOVE حدود _XYZ_C__ (انظر الرسم البياني أدناه).
من خلال إيجاد التقاطع بين \(R_2\) والمنطقة أعلاه , نحصل على حل الجزء في هذه الحالة هو جميع النقاط أعلاه أو على الخط الذي يحتوي على منحدر \(m = -\frac{1}{2}\) وتقاطع y \(n = \frac{3}{4}\).
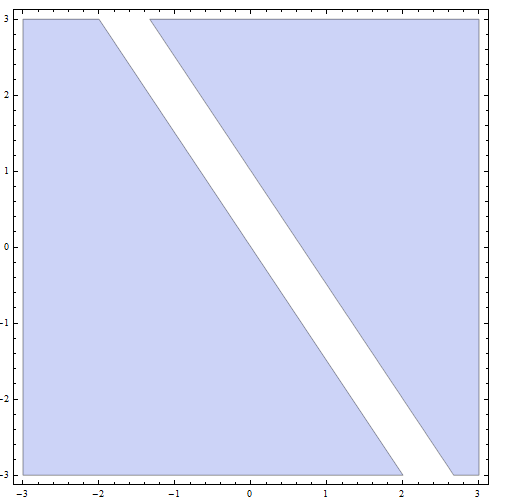
الخطوة الرابعة: الآن , الحل النهائي هو اتحاد جميع حلول الأجزاء من الأجزاء السابقة: الحل النهائي هو جميع النقاط أدناه أو على الخط مع المنحدر \(m = -\frac{1}{2}\) وتقاطع y \(n = -\frac{1}{4}\) , بالإضافة إلى جميع النقاط أعلاه أو على الخط مع المنحدر \(m = -\frac{1}{2}\) وتقاطع ص \(n = \frac{3}{4}\).
بيانيا , نحصل عليه
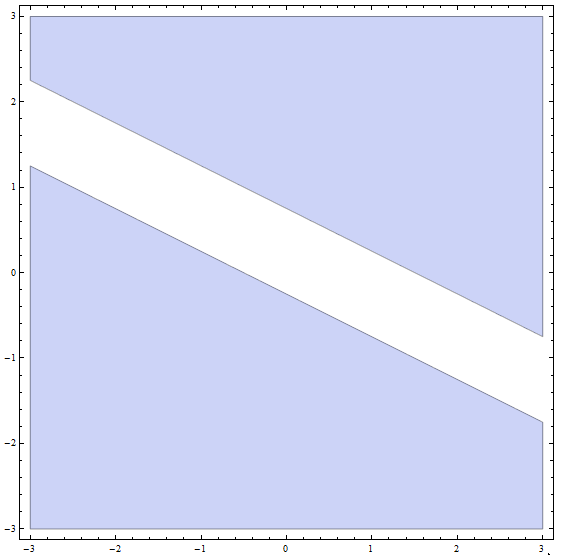
الذي يخلص إلى حل عدم المساواة.
مثال 2
حل متباينة القيمة المطلقة المزدوجة التالية
\[| 2x - 1 | \ge |x + 3|\]إجابه:
هذه قيمة مطلقة مزدوجة لأن هناك قيمتان مطلقتان. هذا يعني أن العثور على المناطق سيستغرق المزيد من العمل (بشكل نسبي).
الخطوة 1: للقيمة المطلقة الأولى التي نحلها:
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]لذلك حصلنا على \(2x- 1 \ge 0\) في \([\frac{1}{2}, +\infty)\) , و \(2x- 1 < 0\) في \((-\infty, \frac{1}{2})\).
للقيمة المطلقة الثانية نحلها:
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]لذلك حصلنا على \(x+3 \ge 0\) في \([-3, +\infty)\) , و \(x+3 < 0\) في \((-\infty, -3)\).
إذن , نحدد 4 مناطق:
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\). في هذه المنطقة نحصل على: \(2x- 1 \ge 0\) و \(x+3 \ge 0\).
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\). في هذه المنطقة نحصل على: \(2x- 1 \ge 0\) و \(x+3 < 0\) , على الرغم من أن هذه المنطقة فارغة.
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\). في هذه المنطقة نحصل على: \(2x- 1 < 0\) و \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\). في هذه المنطقة نحصل على: \(2x- 1 < 0\) و \(x+3 < 0\).
الخطوة 2: نحتاج الآن إلى حل متباينة القيمة المطلقة المزدوجة في كل منطقة من المناطق الأربع:
• في \(R_1\):
هنا نحصل على \(2x- 1 \ge 0\) و \(x+3 \ge 0\) حتى ذلك الحين
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]لذلك , من أجل الحصول على حل الجزء , نحتاج إلى التقاطع مع \(x \ge 4\) , أو \([4, +\infty)\) مع \(R_1\).
وبالتالي فإن حل الجزء المقابل هو: \([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• في \(R_2\):
حل الجزء هذا فارغ (\(\varnothing\)).
• في \(R_3\):
هنا نحصل على \(2x- 1 < 0\) و \(x+3 \ge 0\) حتى ذلك الحين
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]لذلك , من أجل الحصول على حل الجزء هذا , نحتاج إلى تقاطع \( x \le -\frac{2}{3}\) , أو \( (-\infty, -\frac{2}{3}]\) مع \(R_3\).
وبالتالي فإن حل الجزء المقابل هو: \((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• في \(R_4\):
هنا نحصل على \(2x- 1 < 0\) و \(x+3 < 0\) حتى ذلك الحين
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]لذلك , من أجل الحصول على حل الجزء هذا , نحتاج إلى تقاطع \( x \le 4 \) , أو \((-\infty, 4]\) مع \(R_4\).
وبالتالي فإن حل الجزء المقابل هو: \((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
الخطوة الرابعة:
أخيرًا , نحصل على اتحاد الحلول الجزئية , لنحصل على حل المتباينة الأولية المعطاة هو
لم يقل أحد أنها ستكون قصيرة , أليس كذلك؟ حسنا. إنها ليست صعبة حقًا , عليك فقط أن تكون منظمًا وتلتزم بالخطة.
المزيد عن عدم المساواة ذات القيمة المطلقة
لماذا نشعر بالقلق حتى بشأن هذا النوع من عدم المساواة؟ نحن نهتم لأن لديهم تطبيقات في الممارسة.
على سبيل المثال , في الهندسة , يجب تمثيل المسافات في الخط الحقيقي كقيمة مطلقة , لأنها يجب أن تكون غير سالبة.
يمكن للمرء أن يكون لديه موقف هندسي معين حيث تحتاج إلى إيجاد جميع النقاط في الخط الحقيقي التي تكون على الأقل على مسافة 2 من النقطة 3. يمكن وصف هذا الموقف بالمتباينة التالية:
\[| x-3 |\ge 2\]دعونا نفهم عدم المساواة المذكورة أعلاه. النقطة \(x\) هي النقطة التي نريد تحقيق المتباينة فيها. يتم تمثيل المسافة من \(x\) إلى النقطة 3 ب \(|x - 3|\).
بعد ذلك , نحاول إيجاد النقاط التي تكون على الأقل على مسافة 2 من النقطة 3 , لذلك يجب أن تكون المسافة \(|x - 3|\) على الأقل 2 , وهو ما يفسر \(|x - 3| \ge 2.\)
هذا مجرد نوع واحد من مشاكل عدم المساواة في القيمة المطلقة التي يمكنك أن تجدها في الممارسة.
هل يمكنك إيجاد متباينات القيمة المطلقة بدون حل
تتحدى. هنا لديك واحد \(|2x| < |x|\). من الممكن أن تكون عدم المساواة ببساطة غير مجدية مثل هذه التي قدمتها لكم للتو.
ماذا عن الرسم البياني لعدم المساواة في القيمة المطلقة؟
إن عملية رسمها بيانيًا هي في الأساس جنبًا إلى جنب مع عملية حلها: تحتاج إلى العثور على المناطق التي تعرف فيها بالضبط ما إذا كانت حجج القيم المطلقة موجبة أم سلبية , ومن ثم تصبح تفاوتات القيمة المطلقة في متباينات بسيطة , وهو رسم بياني تافه. بعد ذلك , يتم ربط جميع أجزاء المناطق التي تم الحصول عليها ببساطة.