绝对价值不平等
绝对值不等式是存在一个或多个的不等式 绝对值 .让我们回想一下,不等式几乎就像一个等式,但不是“=”符号,而是“≤”或“≥”。
这种差异使得解决方案集通常是一个区域,就像大多数不等式一样。并且涉及绝对值的事实表明对它们的分辨率进行了某种特殊处理。
在本教程中,我们将专注于解决包含一个或多个绝对值的此类不等式所需的特定技能。此外,我们将假设不等式中涉及一两个变量 \(x\) 和/或 \(y\)。
什么是绝对价值不等式？
出于本分析的目的,我们将绝对值不等式视为涉及一个或两个变量且至少具有一个绝对值的不等式。
例如,下面我们有一个绝对值不等式,其中包含两个变量 \(x\) 和 \(y\)：
\[|3x+2y-1| \ge 1\]或者,我们可以得到以下只有一个变量的绝对值不等式：
\[|3x-1| \le 2\]出于我们的目的以及用于解决它们的技术的目的,我们将处理两种类型的不等式（一变量和二变量）
如何解决绝对价值不平等？
在求解方程或不等式时,并没有真正可以解决所有问题的灵丹妙药。每个问题都是不同的,可能有自己的特点。
我们能做的最好的事情就是提供一系列步骤来帮助您解决不等式。
第1步：
对于每个绝对值,确定绝对值的参数为负的区域和非负的区域。
第2步：
如果不等式中只有一个绝对值,则在两个区域（绝对值的参数为负的地方,以及非负的地方）都求解。
第 3 步：
如果不等式中有多个绝对值,则需要将所有区域相交以获得一组较小的分区。在每个分区中,您需要确切地知道每个参数的符号。然后,求解所有区域的不等式。
第四步：
一旦你得到每个领域的部分解决方案,最终的解决方案就是这些部分解决方案的简单联合。
简单来说：您需要找出您确切知道绝对值参数的符号的区域（以便您可以摆脱它们）。
几个例子应该阐明这些步骤。
例 1
解决以下不等式
\[| 2x + 4y - 1 | \ge 2\]回答：
为了解决不等式,我们需要使用上面指定的步骤。
第1步： 绝对值只有一个,所以我们需要判断参数是否为负数和非负数。因此,我们需要先解决：
\[2x + 4y - 1 \ge 0\]有几种策略可以解决上述问题,但最简单的一种是先解方程
\[2x + 4y - 1 = 0\]这意味着 \(4y = -2x + 1\) 或与 \(y = -\frac{1}{2}x + \frac{1}{4}\) 相同,它对应于具有斜率 \(m = -\frac{1}{2}\) 和 y 截距 \(n = \frac{1}{4}\) 的线。
现在,为了处理 \(2x + 4y - 1 \ge 0\),我们测试点 \((0,0)\) 是否满足不等式：
\[2(0) + 4(0) - 1 = -1 < 0\]所以,\((0,0)\) 是否满足不等式。结论是具有斜率 \(m = -\frac{1}{2}\) 和 y 截距 \(n = \frac{1}{4}\) 的线将平面划分为两个区域：
对于线以下的点（我们称这个区域为 1,\(R_1\)）,我们得到 \(2x + 4y - 1 < 0\)
对于线上方的点,包括线本身（我们称此区域为 2,\(R_2\)）,我们得到 \(2x + 4y - 1 \ge 0\)
为什么这很重要？为什么我们要承担这些麻烦？因为在 \(R_1\) 上,我们得到了,因为 \( 2x + 4y - 1 < 0\),然后是 \(| 2x + 4y - 1 | = -(2x + 4y - 1) \)。类似地,在 \(R_2\) 上,我们得到了,因为 \( 2x + 4y - 1 \ge 0\),然后是 \(| 2x + 4y - 1 | = 2x + 4y - 1 \)。
第2步： 现在我们需要解决区域 1 上的不等式,\(R_1\) ：
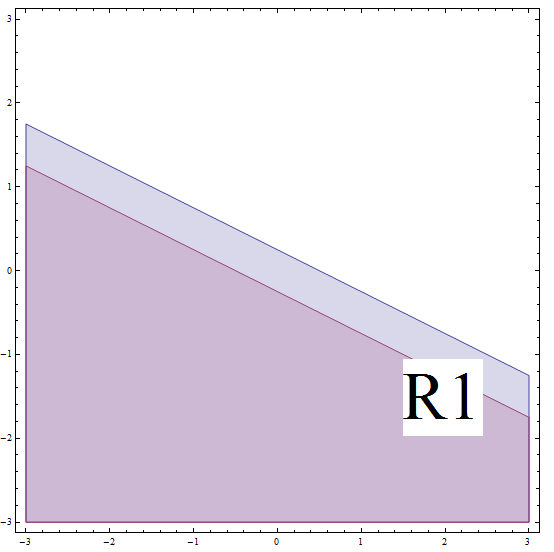
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow -(2x + 4y - 1) \ge 2\] \[\Rightarrow 2x + 4y - 1 \le -2 \text{ (multiplying by (-1) changes the direction of the inequality)}\] \[\Rightarrow 2x + 4y \le -1\] \[\Rightarrow 4y \le -2x - 1\] \[\Rightarrow y \le -\frac{1}{2}x - \frac{1}{4} \]这对应于斜率为 \(m = -\frac{1}{2}\) 和 y 截距 \(n = -\frac{1}{4}\) 的直线下方或线上的所有点。但是不要忘记您在 \(R_1\) 上,我们发现的这条线在 \(R_1\) 的边界以下（见下图）。
澄清一下,因为我们假设我们在 \(R_1\),所以我们需要让我们在斜率为 \(m = -\frac{1}{2}\) 和 y 截距 \(n = \frac{1}{4}\) 的直线下方。在这个假设下,我们解决了原始的不等式,我们还需要低于斜率 \(m = -\frac{1}{2}\) 和 y 截距 \(n = -\frac{1}{4}\) 的线。这两个条件必须同时发生,所以我们得到两个区域的交集。
那么,在这种情况下,部分解对应于斜率为 \(m = -\frac{1}{2}\) 和 y 截距 \(n = -\frac{1}{4}\) 的直线下方或线上的所有点。
现在我们需要解决区域 2 上的不等式,\(R_2\) ：
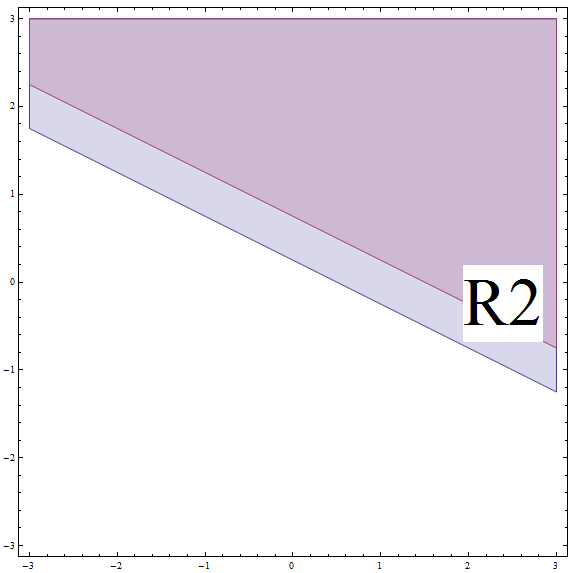
\[| 2x + 4y - 1 | \ge 2\] \[\Rightarrow 2x + 4y - 1 \ge 2\] \[\Rightarrow 2x + 4y \ge 3\] \[\Rightarrow 4y \ge -2x + 3\] \[\Rightarrow y \ge -\frac{1}{2}x + \frac{3}{4} \]这对应于斜率为 \(m = -\frac{1}{2}\) 和 y 轴截距为 \(n = \frac{3}{4}\) 的直线上方或线上的所有点。但不要忘记你在 \(R_2\) 上,这条线在 \(R_2\) 的边界之上（见下图）。
通过找到 \(R_2\) 和上面区域之间的交点,我们得到在这种情况下的部分解是上面或在斜率为 \(m = -\frac{1}{2}\) 和 y 截距 \(n = \frac{3}{4}\) 的线上的所有点。
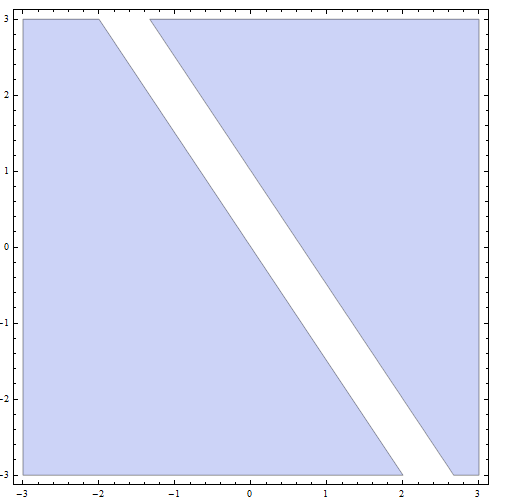
第四步： 现在,最终解是前面部分的所有部分解的并集：最终解是所有位于 BELOW 或斜率为 \(m = -\frac{1}{2}\) 和 y 轴截距 \(n = -\frac{1}{4}\) 的线上的所有点,加上所有 ABOVE 或斜率为 \(m = -\frac{1}{2}\) 的线上的点和 y 截距 \(n = \frac{3}{4}\)。
图形上,我们得到
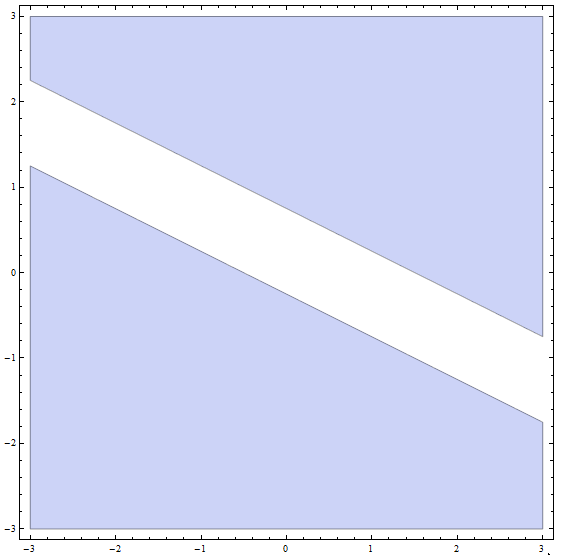
这就结束了不等式的解决。
例2
解决以下双重绝对值不等式
\[| 2x - 1 | \ge |x + 3|\]回答：
这是一个双绝对值不等式,因为有 2 个绝对值。这意味着找到这些区域需要做更多的工作（相对而言）。
第1步： 对于第一个绝对值,我们求解：
\[2x- 1 \ge 0\] \[\Rightarrow \,\, 2x \ge 1\] \[\Rightarrow \,\, x \ge \frac{1}{2}\]所以我们在 \([\frac{1}{2}, +\infty)\) 上得到了 \(2x- 1 \ge 0\),在 \((-\infty, \frac{1}{2})\) 上得到了 \(2x- 1 < 0\)。
对于第二个绝对值,我们求解：
\[x+3 \ge 0\] \[\Rightarrow \,\, x \ge -3\]所以我们在 \([-3, +\infty)\) 上得到了 \(x+3 \ge 0\),在 \((-\infty, -3)\) 上得到了 \(x+3 < 0\)。
那么,我们定义了 4 个区域：
\(R_1 = [\frac{1}{2}, +\infty) \cap [-3, +\infty) = [\frac{1}{2}, +\infty)\)。在这个区域,我们得到：\(2x- 1 \ge 0\) 和 \(x+3 \ge 0\)。
\(R_2 = [\frac{1}{2}, +\infty) \cap (-\infty, -3) = \varnothing\)。在这个区域我们得到：\(2x- 1 \ge 0\) AND \(x+3 < 0\),尽管这个区域是空的。
\(R_3 = (-\infty, \frac{1}{2}) \cap [-3, +\infty) = [-3, \frac{1}{2})\)。在这个区域我们得到： \(2x- 1 < 0\) 和 \(x+3 \ge 0\)
\(R_4 = (-\infty, \frac{1}{2}) \cap (-\infty, -3) = (-\infty, -3)\)。在这个区域,我们得到：\(2x- 1 < 0\) 和 \(x+3 < 0\)。
第2步： 现在我们需要解决四个区域中每个区域的双重绝对值不等式：
• 在 \(R_1\) 上：
在这里我们得到 \(2x- 1 \ge 0\) 和 \(x+3 \ge 0\) 那么
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, 2x - 1 \ge x + 3\] \[\Rightarrow \,\, 2x - x \ge 3 - (-1)\] \[\Rightarrow \,\, x \ge 4\]因此,为了获得零件解决方案,我们需要将 \(x \ge 4\) 或 \([4, +\infty)\) 与 \(R_1\) 相交。
因此对应的部分解为：\([\frac{1}{2}, +\infty) \cap [4, +\infty) = [4, +\infty)\)
• 在 \(R_2\) 上：
这部分解决方案是空的 (\(\varnothing\))。
• 在 \(R_3\) 上：
在这里我们得到 \(2x- 1 < 0\) 和 \(x+3 \ge 0\) 那么
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge x + 3\] \[\Rightarrow \,\, 2x - 1 \le -x - 3\] \[\Rightarrow \,\, 2x - (-x) \le -3 - (-1)\] \[\Rightarrow \,\, 3x \le -2\] \[\Rightarrow \,\, x \le -\frac{2}{3}\]因此,为了获得这部分解决方案,我们需要将 \( x \le -\frac{2}{3}\) 或 \( (-\infty, -\frac{2}{3}]\) 与 \(R_3\) 相交。
因此对应的部分解为：\((-\infty, -\frac{2}{3}] \cap [-3, \frac{1}{2}) = [-3, -\frac{2}{3}] \)
• 在 \(R_4\) 上：
在这里我们得到 \(2x- 1 < 0\) 和 \(x+3 < 0\) 那么
\[| 2x - 1 | \ge |x + 3|\] \[\Rightarrow \,\, -(2x - 1) \ge -(x + 3)\] \[\Rightarrow \,\, 2x - 1 \le x + 3\] \[\Rightarrow \,\, 2x - x \le 3 - (-1)\] \[\Rightarrow \,\, x \le 4\]因此,为了获得这部分解决方案,我们需要将 \( x \le 4 \) 或 \((-\infty, 4]\) 与 \(R_4\) 相交。
因此对应的部分解为：\((-\infty, -3) \cap (-\infty, 4] = (-\infty, -3) \)
第四步：
最后,我们得到部分解的并集,得到初始给定不等式的解为
没人说会短路吧？好。这并不难,您只需要系统化并坚持计划即可。
更多关于具有绝对值的不平等
为什么我们甚至担心这种不平等？我们关心,因为他们在实践中确实有应用程序。
例如,在几何中,实线中的距离需要表示为绝对值,因为它必须是非负的。
可能有一种几何情况,你需要在实线上找到所有距离点 3 至少为 2 的点。 这种情况可以用以下不等式来描述：
\[| x-3 |\ge 2\]让我们理解上面的不等式。点 \(x\) 是我们想要满足不等式的点。从 \(x\) 到点 3 的距离由 \(|x - 3|\) 表示。
然后,我们试图找到距离点 3 至少为 2 的点,因此距离 \(|x - 3|\) 需要至少为 2,这就解释了 \(|x - 3| \ge 2.\)
这只是您在实践中可以找到的一种绝对值不等式问题。
你能找到无解的绝对值不等式吗
你打赌。这里有一个 \(|2x| < |x|\)。一个不等式可能像我刚刚给你的这个例子一样根本不可行。
如何绘制绝对值不等式？
绘制它们的过程本质上与求解它们的过程密切相关：您需要找到您确切知道绝对值的参数是正还是负的区域,然后绝对值不等式变成简单的不等式,这是简单的图形。然后,将获得的所有区域简单地连接起来。