二项式定理
二项式定理是代数中最著名的定理之一,它在代数,概率和统计领域有很多应用。它为 n 陈述了一个漂亮而简洁的公式 日 两个值之和的幂:\((a+b)^n\)
![]() 1665 年,艾萨克·牛顿爵士首次非正式地介绍了我。
1665 年,艾萨克·牛顿爵士首次非正式地介绍了我。
![]() 许多其他著名的数学家在牛顿之后解决了二项式定理。在 17 和 18 世纪,这是一个非常吸引人的问题。
许多其他著名的数学家在牛顿之后解决了二项式定理。在 17 和 18 世纪,这是一个非常吸引人的问题。
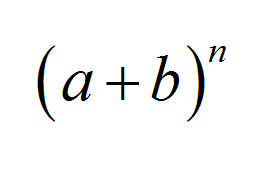
二项式展开的公式
二项式定理的整数之处在于它提供了一个非常优雅和简洁的公式。在进入公式之前,让我们做一些计算。例如,对于 \(n = 2\) 我们得到:
\[\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2 \] \[\large = a^2 + 2ab + b^2 \]现在让我们尝试使用 \(n = 3\):
\[\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b) \] \[\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3 \] \[\large = a^3 + 3a^2b + 3ab^2 + b^3\]最后,让我们勇敢地用 \(n = 4\) 试试吧:
\[\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b) \] \[\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4 \] \[\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4\]好吧,那很勇敢,对吧??你在那里看到任何图案。我能看到一些。例如,对于 \(n = 2\),我们可以将其简化为 3 项。对于 \(n = 3\) 我们可以将其简化为 4 项,对于 \(n = 4\) 我们可以将其简化为 5 项。所以总的来说,我预计对于 \(n\) 的一般幂,我们会有 \(n+1\) 项
更多图案?好吧,总有一个形式为 \(a^l b^m\) 的项,我们可以看到 \(l\) 的幂在减少,而 \(m\) 的幂在增加。但也有一些有趣的事情:如果你检查每一项,权力的总和总是 \(n\)。实际上,您将检查所有这些术语的 \(l + m = n\)。
例如,对于 \(n = 2\),您有术语 \(2 a b\)。 \(a\)的幂为1,\(b\)的幂为1,幂的和为\(1 + 1 = 2\)。或者例如,对于 \(n = 4\),你有 \(6 a^2 b^2\) 项,其中 \(a\) 的幂是 2,而 \(b\) 的幂是 2,幂的总和是 \(2 + 2 = 4\)
一般二项式定理
现在我们准备给出二项式定理的一般表达式。准备好?我们有:
\[\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n \]其中术语 \({n \choose i}\) 读作“n 选择 i”或“组合系数”,它被定义为
\[\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}\]例如,
\[\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10\]你可以用这个 组合系数计算器 通过查看显示的所有步骤来了解有关它的更多信息并进行练习。
使用求和的一般二项式定理
上面定义二项式定理的总和通过扩展使用符号,使这些术语更易于理解。像在数学中一样,我们试图让事情更紧凑,上面的表达式可以总结为:
\[\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i} \]观察展开式中项的幂。通用术语是 \(a^i b^{n-i}\)(乘以常数)。权力的总和是 \(i + (n-i) = n\)。所以展开式中所有项的幂之和必须是 \(n\)。是不是很漂亮???
例 1
\(x^3 y^2\) 项(乘以常数)能否成为 \((x+y)^6\) 扩展的一部分?为什么?
回答:
答案是不。在这种情况下,\(n = 6\),我们从二项式定理知道,展开式中 \(x^l y^m\) 项的幂之和必须等于 \(n\)。在这种情况下,\(l + m = 3 + 2 = 5\) 与 \(n = 6\) 不同。因此,术语 \(x^3 y^2\)(乘以常数)不能是 \((x+y)^6\) 扩展的一部分。
例2
使用二项式定理展开 \((a-b)^3\)。
回答:
等待。你一定在想“你刚刚教我如何扩展 \((a+b)^n\),但现在你问我 \((a-b)^n\)。你为什么这么残忍”。坚持,稍等。我不是在捉弄你。
总有一个技巧(不要忘记那条线,它经常出现在数学中)。
![]() 观察到 \(a - b\) 与 \(a + (-b)\) 相同。
观察到 \(a - b\) 与 \(a + (-b)\) 相同。
Ahhhhhhh,所以二项式定理仍然适用。那么:
\[\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3 \] \[\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3 \] \[\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3 \] \[\large = a^3 - 3 a^2 b + 3 a b^2 -b^3 \]关于二项式展开的更多信息
二项式定理非常重要,几乎所有课程都涵盖了它,包括代数,微积分,概率和统计。
有一些概括,如负二项式展开,这超出了本教程的范围。
帕斯卡三角
有时,当学生需要计算二项式展开式中的常数(组合系数)时,他们会陷入困境。一种非常简单的方法是使用帕斯卡三角形。
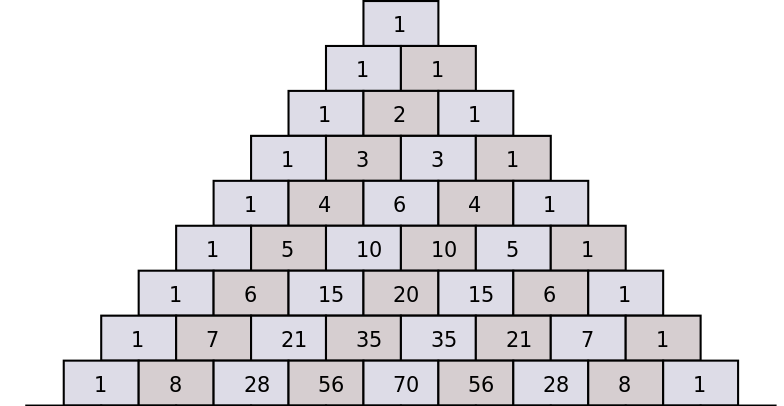
帕斯卡三角形显示了如何根据 \(n\) 的先前值的系数,通过添加紧接在上面的两个系数来计算连续二项式系数。
应用
二项式展开在代数和概率论中有多种应用。例如,在概率中,二项式分布基于二项式定理。
事实上,考虑一个数字 \(0 \le p \le 1\)。然后, \(p + (1-p) = 1\) 我们可以使用二项式定理:
\[\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} \]意思就是
\[\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1 \]事实证明,每个 \({n \choose i} p^i (1-p)^{n-i}\) 项都代表一个概率。此外,我们还有:
\[\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1 \]其中 \(X\) 是 \(n\) 次试验后的成功次数,此时每次试验的成功概率为 \(p\)。 \(X\) 变量称为二项式随机变量。
相关计算器
你也可以 使用此计算器计算二项式分布的概率 .此外,您可能想要计算 置换系数 , 与组合系数有关。
