Z-Critical Values Calculator

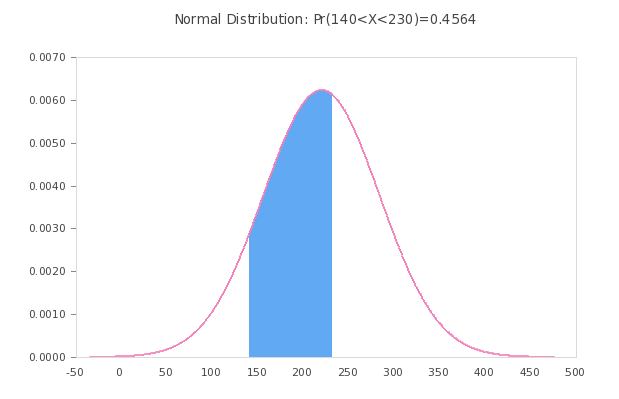
Some more information about critical values for the normal distribution probability : First of all, critical values are points at the tail(s) of a certain distribution and the property of these values is that that the area under the curve for those points to the tails is equal to the given value of \(\alpha\).

Properties of the Normal Distribution

For a two-tailed case, the critical values correspond to two points to the left and right of the center of the distribution.

They will have the property that the sum of the area under the curve for the left tail (from the left critical point) and the area under the curve for the right tail is equal to the given significance level \(\alpha\).

For a left-tailed case, the critical value corresponds to the point to the left of the center of the distribution. They will have the the property that the area under the curve for the left tail (from the critical point to the left) is equal to the given significance level \(\alpha\).

In the case of a right-tailed, the critical value corresponds to the point to the right of the center of the distribution. They will have the property that the area under the curve for the right tail (from the critical point to the right) is equal to the given significance level \(\alpha\)

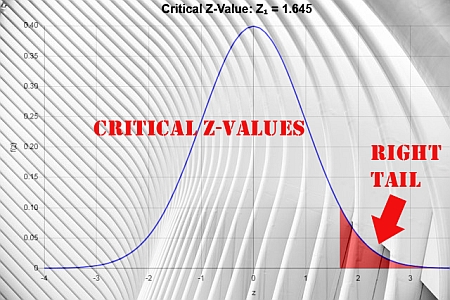
Critical Values Normal Distribution

The main properties are:

• If the distribution being analyzed is symmetric, the critical points for the two-tailed case are symmetric with respect to the center of the distribution


• For a symmetric distribution, finding critical values for a two-tailed test with a significance of \(\alpha\) is the same as finding one-tailed critical values for a significance of \(\alpha/2\).

Alternatively to using this calculator, you can use a z critical value table to find the values you need. Such tables typically come along with most Stats textbooks. It is indeed a good exercise to learn how to use those tables.

A similar type of critical value can be computed for the t-distribution. So use the following calculator if you need to compute critical t-values .

How to Compute Critical Z-values

You can either use a z critical value table, normally found in the back of the college Statistics books.

Or you can use this calculator, which will find the critical value using Stats libraries and it will give you a graph depiction of the corresponding critical values.

Finding critical z values is crucial for conducting z-tests, where a normal distribution calculator is used to assess whether or not the z-test statistics is sufficiently extreme to reject the null hypothesis.