Z-Score Calculator
Instructions: Use this Z-score calculator to compute, showing all the steps, the Z-score associated with a raw score X. Please provide the information required below about the population mean \(\mu\) and population standard deviation \(\sigma\):
How to Use This Z-Score Calculator
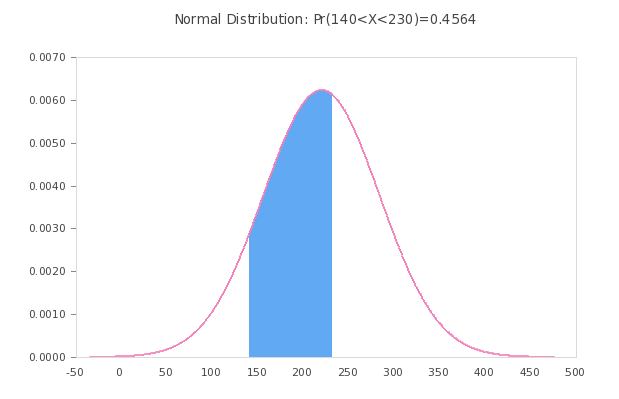
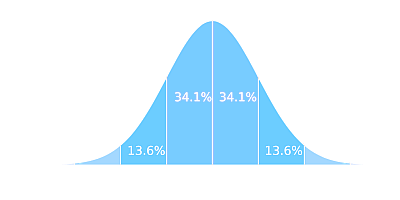
More about this z-score calculator with steps, with a little background: The normal probability is a type of continuous probability distribution that can take random values on the whole real line.
The idea of using z-score is to asses how far a score is from the mean, relative to the size of the standard deviation. This is, the deviation of a score from the mean is normalized with respect to the standard deviation.
How to Compute Z-scores?
A random variable X that has a normal distribution with mean \(\mu\) and standard deviation \(\sigma\) can be standardized or normalized to a standard normal distribution (with mean 0 and standard deviation 1), by using the following formula:
\[ z = \frac{X-\mu}{\sigma} \]This is exactly what this z score calculator with steps will do for you if you type the parameters in the form above.
Observe that the numerator is called the deviation score .
Z-score calculator sample
For example, say you have a raw score of \(X = 20\) in a population where you know that the population mean is \(\mu = 15\) and population standard deviation is \(\sigma = 1\).
Then, in the box above that says "Population Mean" you will type "15". In the box above that says "Population St. Dev" you will type "5", and finally, in the box that says "Raw Score" you will type "20". Then you press "Calculate" and the solver will show step-by-step calculations.
Calculating a Raw score from a z-score
Now, the inverse process would consist of calculating a raw score associated to a z-score, in which case you should use this calculator .
The above is referred to the z-score associated to the original X score. Another common operation you may be interested in is to compute critical z-values . Also, you may want to use our z score calculator area .
Another procedure you may be interested in the to convert z-scores to percentiles , which is at the bottom of the role of the normal probability tables, where z-scores are linked to probabilities, which in term are associated to percentiles.
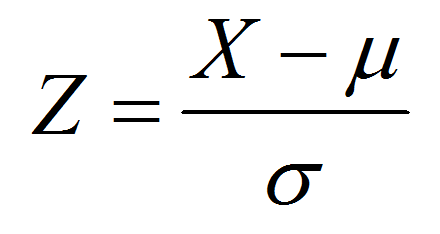
Finding outliers
Z-scores are sometimes used to find outliers by identifying z-scores that have an absolute value above 2. But z-scores are too sensitive to extreme values, so you in order to find outliers you can use this calculator, that uses quartiles instead.