Spearman Correlation Calculator
Instructions: You can use this Spearman Correlation Calculator tool to compute Spearman's Correlation Coefficient for two variables X and Y. All you have to do is type your X and Y data, or simply paste it from Excel or another source.
More about the Spearman correlation coefficient
The correlation coefficient calculated above corresponds to Spearman's correlation coefficient. The requirements for computing it is that the two variables X and Y are measured at least at the interval level (which means that it does not work with nominal or ordinal variables).
How do you calculate Spearman's rank correlation?
The formula for Pearson's correlation coefficient is:
\[r_S =\frac{n \sum_{i=1}^n Rank(x_i) Rank(y_i) - \left(\sum_{i=1}^n Rank(x_i) \right) \left(\sum_{i=1}^n Rank(y_i) \right) }{\sqrt{n \sum_{i=1}^n Rank(x_i)^2 - \left( \sum_{i=1}^n Rank(x_i) \right)^2} \sqrt{n \sum_{i=1}^n Rank(y_i)^2 - \left( \sum_{i=1}^n Rank(y_i) \right)^2} }\]or equivalently
\[r_S = \frac{SS_{\tilde X \tilde Y}}{\sqrt{SS_{\tilde X \tilde X}\cdot SS_{\tilde Y \tilde Y} }}\]A great way of seeing this process is to first find the rank associated with each of the values in the sample, and then you use the formula used for Pearson's correlation to find the correlation of those ranks.
For interval level data, you should use Pearson's correlation coefficient calculator instead. Also, to graphically visualize the data and understand better the linear association between the variables X and Y, you can use our scatterplot maker
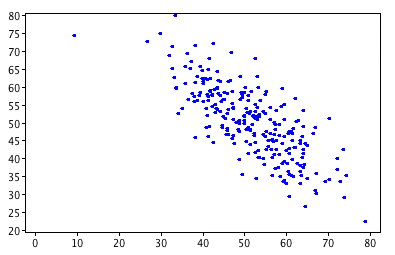
Reporting Spearman's Rank Correlation
How to report Spearman's correlation? Very similarly to the way it is reported for the case of Pearson's correlation. Typically you will write something like: "The ordinal variables X and Y show a significant degree of linear association, \(r_s = .894, p < .001\)."
How to assess whether or not Spearman's correlation is significant?
The most common way to assess whether or not the observed value of Spearman's correlation is significant is to compare with the corresponding Spearman's critical values . Alternatively, in order to find critical correlation values you can use a specialized table, that sometimes comes in Stats textbooks.