Question: 0.5X₁ + 1.5X₂ + 1X₃ \(\le \) 450 (steel, lbs)

1X₁ + 1X₂ + 1X₃ \(\le \) 430 (aluminum, lbs)

1X₁ + 0.1X₂ + 0.2X₃ \(\le \) 80 (forming, hrs)

0.3X₁ + 0.2X₂ + 0.1X₃ \(\le \) 50 (assembly, hrs)

X₁,X₂,X₃ \(\ge \) 0

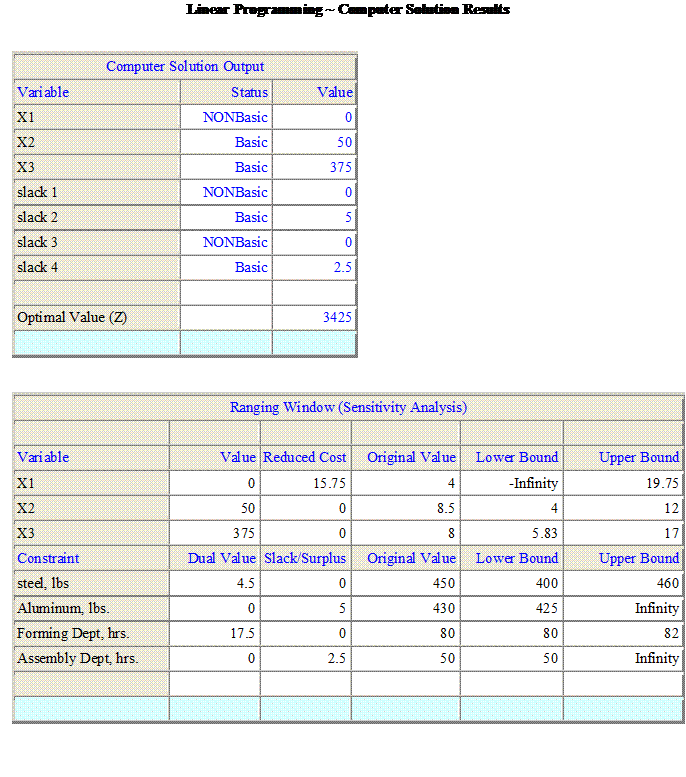Using the computer solution output, answer the following questions.

a. What is the optimal daily production plan for Metallica? That is, how many Baron, Secretary, and Executive chairs each, Metallica should produce daily in order to maximize their profit.

b. What would the firm's optimal profit be?

c. Which Metallica resources are unused at the end of each day’s shift?

d. Would you support a 2-hour reduction in the amount of hours available in the assembly department? Why or why not?

e. Would you support a 5-lb increase in daily steel availability at a cost of $4.00 per lb.? Why or why not?

f. If the profit from each Baron chair changed from $4.00 to $10.00, would the company’s daily optimal production plan change? Explain.

g. Would you support asking an employee in the forming dept to work overtime for one hour each day at the total cost of $14 per hour? Why or why not?

h. Suppose that 4lbs of aluminum supplied on a given day are bad, what would the full impact of this on output and or profit?