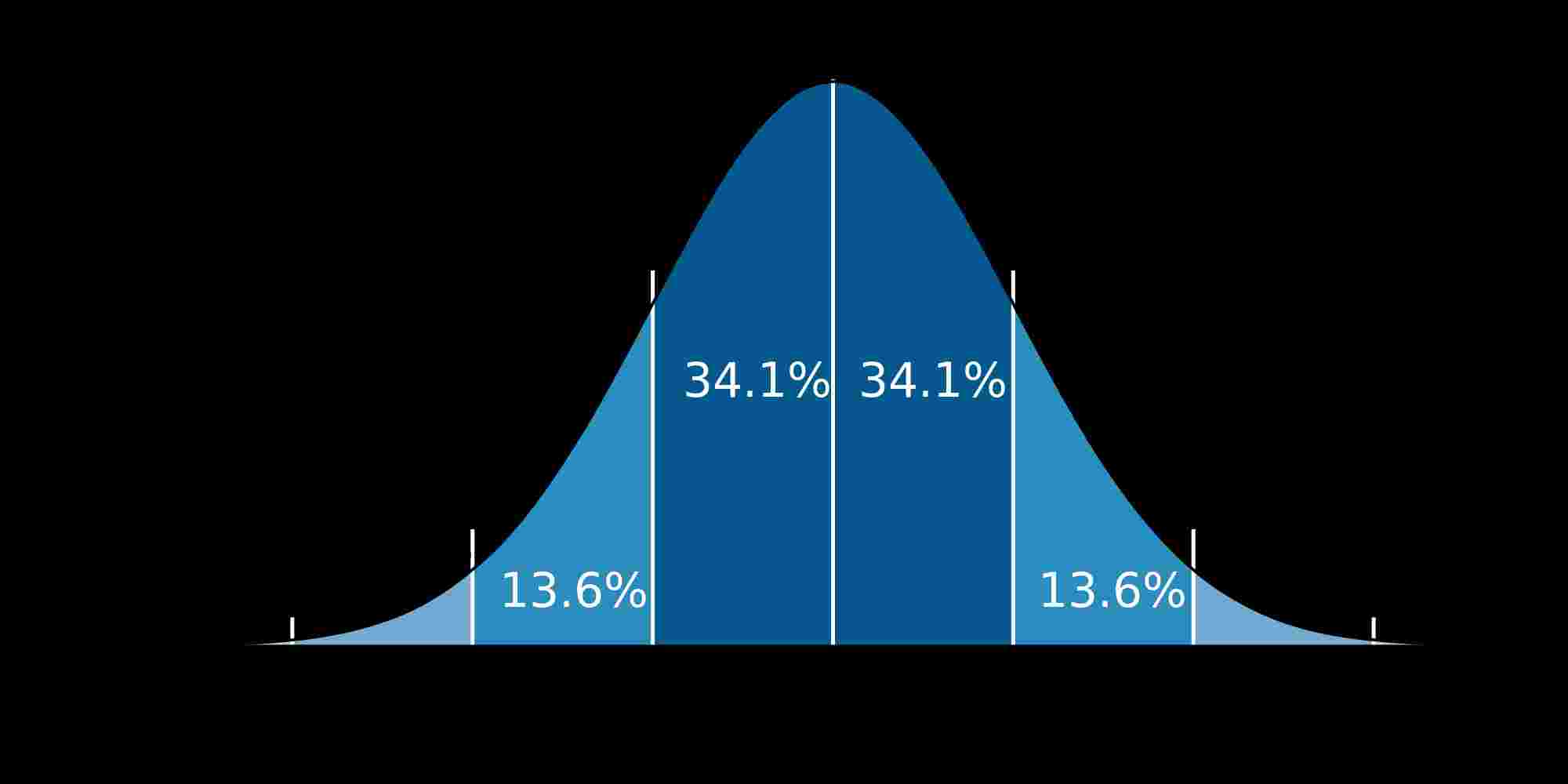
[Step-by-Step] The grade point averages (GPAs) of all students enrolled at a large university have a normal distribution with a population mean of 3.02
Question: The grade point averages (GPAs) of all students enrolled at a large university have a normal distribution with a population mean of 3.02 and a population standard deviation of 0.29. A random sample of 16 students is drawn from the Registrar’s list. For part (a), be sure to use the z-calculation that is for sample means. I am presenting it to steer you in the right direction:
Z = \[(\bar{x}\] - )/(/ \[\sqrt{n}\] ).
It is important that you understand this expression. See the text starting on page 261.
- What is the probability that the sample mean GPA calculated from your random sample of 16 students is 3.10 or higher?
- What is the probability that the GPA of an individual randomly selected from the Registrar’s list is 3.10 or higher?
- Why do I need to state that the distribution of GPAs for individual students is normal in order to do part (a) of this problem? Please answer in a single sentence.
Deliverable: Word Document 



![[Solution Library] What is the probability of drawing 2 balls, in [Solution Library] What is the probability of](/images/solutions/MC-solution-library-37003.jpg)
![[Solution] If only one ball is drawn, what is the probability that [Solution] If only one ball is drawn,](/images/solutions/MC-solution-library-37004.jpg)