Stats Solutions

(See Solution) An 11-m beam is subjected to a load, and the shear force follows the equation V(x)=5+0.25 x^2 where V is the shear force, and x is length

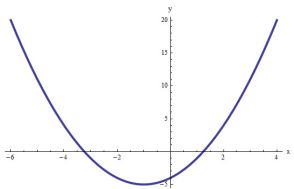
Question: An \(11-\mathrm{m}\) beam is subjected to a load, and the shear force follows the equation

\[V(x)=5+0.25 x^{2}\]

where \(V\) is the shear force, and \(x\) is length in distance along the beam. We know that \(V=d M / d x\), and \(M\) is the bending moment. Integration yields the relationship

\[M=M_{o}+\int_{0}^{x} V d x\]

If \(M_{o}\) is zero and \(x=11\), calculate \(M\) using (a) analytical integration, (b) multiple-application trapezoidal rule. For (b) use 1-m increments.

Price: $2.99
Solution: The downloadable solution consists of 1 pages
Deliverable: Word Document


∴ Other downloads you may be interested in ∴

log in to your account

Forgot password?
Don't have a membership account?
REGISTER

reset password

Back to
log in

sign up

Back to
log in