Radians To Degrees
Instructions: Use this radians to degrees calculator with steps to convert an angle in radians to degrees. All you have to do is type the angle in radians, and the calculator will show you how to convert it to degrees, showing all the steps:
More About Radians to Degrees Conversion
What are radians and why we want to convert them into degrees? In the end, all angle measures are arbitrary, and and are tied to how big an opening of two rays with a common origin opening is. Indeed, angles refer to a measure of the opening between to line segments with respect to the circle
What are the different reference systems to measure angles?
When we measure an angle in degrees, an angle of 360 o corresponds to the full opening of a circle. All other angles that are measured in degrees will be proportional to the amount of the opening associated for the angle.
For example, if the opening of the angle corresponds to half opening of the circle, the angle will be half of what is for the full opening, this is half of 360 o , which is 180 o
Measuring angles as radians
Another system to measure angles the radians system, which utilizes a different approach, but yet it is the same principle. In this case, the angle depends on the opening, but this opening is measured based on how many radiuses are represented by the arc length of the segment in the circle that is determined by the corresponding angle.
We know that the full opening of the circle has a perimeter of \(2\pi\), which otherwise said indicates that we can fit \(2\pi\) radiuses in the full opening of the circle, and this indicates that the full opening of the circle corresponds to \(2\pi\) radians.
Why do we really use radians?
There is always the question of why even use radians, or even, why use more than one convention for measuring angles. There are several reasons for that:
- The degrees system is an old Mesopothamian convention, which is not necessarily rooted in anything relevant.
- The radian system is indeed a much more intuitive method, because it ties the angle to the number perimeter formed by the angle
- Excel and most scientific software use angles in radians by default, because of the more natural calculus properties trigonometric functions have when when the angle argument is measured in radians
How to Convert Radians to Degrees?
So, what is the formula to convert radians to degrees? If you have an angle that is measured as \(r\) in radians, the angle in degrees \(d\) is computed as follows:
\[d = \frac{360 r}{2\pi} = \frac{180 r}{\pi} \]The above formula applies whether you are converting decimals or fraction radians to degree. All you need to do is to plug the number of radians \(r\) into the formula
Example 1: Convert \(\pi\) radians into degrees.
Solution: All you need to do is to plug \(r\) into the above formula. In this case, \(r = \pi\) radians, so we get
\[d = \frac{180 r}{\pi} = \frac{180 \cdot \pi}{\pi} = 180^{o} \] so then \(\pi\) radians corresponds to 180 o degrees.Example 2: Now convert \(\displaystyle \frac{3\pi}{4}\) radians into degrees.
Solution: Same as with the previous example, we need to plug \(r\) into the above formula. In this case, \(\displaystyle r = \frac{3\pi}{4}\) radians, so we get
\[d = \frac{180 r}{\pi} = \frac{180 \cdot \frac{3\pi}{4}}{\pi} = 135^{o} \] so then \(\displaystyle \frac{3\pi}{4}\) radians corresponds to 135 o degrees.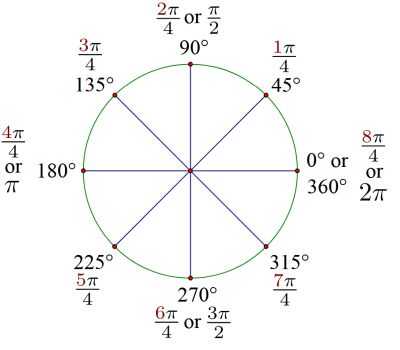
How to use Excel for Angle Conversions
For those of you who work with Excel, you can use the function "=DEGREES(r)" to convert an angle in radians to degrees.
Can you have a Degrees to radians chart?
You definitely have one, but in reality, there are infinite angles, so you won't be able to have a table long enough. Perhaps it would be a good idea to have a table with the corresponding association of notable angles between degrees and radians.
For example, it would be convenient to have pairs like 90o -> \(\pi/2\), 45o -> \(\pi/4\), so to get quick access to the most commonly used angles.
More calculators related to angles
There are occasions in which you would use a calculator other than this radian calculator. For example, if conversely you can to convert degrees of radians for the case you have an angle that is given in degrees, you should use this other calculator .
You can explore other trigonometric calculators, many of them related to angles, such as our double angle calculator , among many others.